题目内容
【题目】如图:抛物线y=x2+bx+c与直线y=﹣x﹣1交于点A,B.其中点B的横坐标为2.点P(m,n)是线段AB上的动点.
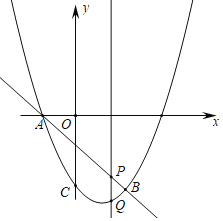
(1)求抛物线的表达式;
(2)过点P的直线垂直于x轴,交抛物线于点Q,求线段PQ的长度l与m的关系式,m为何值时,PQ最长?
(3)在平角直角坐标系中,我们把横、纵坐标都为整数的点称为整点,记顶点都是整点的四边形为整点四边形,在(2)的情况下,在平面内找出所有符合要求的整点R,使P、Q、B、R为整点平行四边形,请直接写出整点R的坐标.
【答案】(1)y=x2﹣2x﹣3;(2)l=﹣m2+m+2,当m=![]() 时,PQ最长,最大值为
时,PQ最长,最大值为![]() ;(3)符合条件的点R有,它的坐标为(2,﹣1)或(2,﹣5)或(0,﹣3)或(﹣2,﹣1).
;(3)符合条件的点R有,它的坐标为(2,﹣1)或(2,﹣5)或(0,﹣3)或(﹣2,﹣1).
【解析】
(1)先由一次函数解析式求出A,B两点的坐标,再根据待定系数法,可得抛物线的解析式;
(2)根据平行于y轴直线上两点间的距离是较大的纵坐标减较小的纵坐标,可得二次函数,根据二次函数的性质,可得答案;
(3)使P,Q,B,R为顶点的四边形是平行四边形,可以分两种情况:一是PQ为一边时,根据PQ的长是正整数,可得PQ,根据平行四边形的性质,对边平行且相等,根据点的坐标表示方法,可得答案,二是PQ为一条对角线时,根据平行四边形的性质,PQ与BR互相平分,此时R与C 重合.
(1)∵抛物线y=x2+bx+c与直线y=﹣x﹣1交于点A,B,
∴当y=0时,﹣x﹣1=0,
解得x=﹣1,
∴A(﹣1,0),
∵点B的横坐标为2,
∴﹣x﹣1=﹣2﹣1=﹣3,
∴B(2,﹣3),
将A(﹣1,0),B(2,﹣3)代入y=x2+bx+c得:
![]() ,
,
解得,![]() ,
,
∴抛物线的解析式为:y=x2﹣2x﹣3;
(2)∵点P在直线AB上,Q抛物线上,P(m,n),
∴n=﹣m﹣1,Q(m,m2+2m﹣3)
∴PQ的长l=(﹣m﹣1)﹣(m2﹣2m﹣3)=﹣m2+m+2,
∴当m=![]() =
=![]() 时,PQ的长l最大=﹣
时,PQ的长l最大=﹣![]() +
+![]() +2=
+2=![]() .
.
答:线段PQ的长度l与m的关系式为:l=﹣m2+m+2,当m=![]() 时,PQ最长,最大值为
时,PQ最长,最大值为![]() ;
;
(3)由(2)可知,0<PQ≤![]() .
.
①当PQ为边时,BR∥PQ且BR=PQ.
∵R是整点,B(2,﹣3),
∴PQ是正整数,
∴PQ=1,或PQ=2.
当PQ=1时,
﹣m2+m+2=1,
∴m=![]() ,
,
此时P,Q不是整点,不合题意舍去,
当PQ=2时,
﹣m2+m+2=2,
∴m1=0,m2=1,
∵BR=2,此时点R的横坐标为2,
∴纵坐标为﹣3+2=﹣1或﹣3﹣2=﹣5,
即R(2,﹣1)或R(2,﹣5).
②当PQ为平行四边形的一条对角线,则PQ与BR互相平分,
当PQ=1时,即:﹣x﹣1﹣(x2﹣2x﹣3)=1,此时x不是整数,
当PQ=2时,即﹣x﹣1﹣(x2﹣2x﹣3)=2,此时x1=﹣1,x2=0;
∴x1=﹣1,R与点C重合,即R(0,﹣3),
x2=0;此时R(﹣2,﹣1).
综上所述,符合条件的点R有,它的坐标为(2,﹣1)或(2,﹣5)或(0,﹣3)或(﹣2,﹣1).

 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案