题目内容
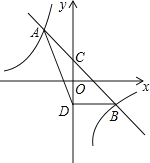
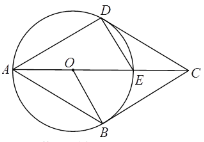
【题目】如图,已知四边形ABCD中,E是对角线AC上一点,DE=EC,以AE为直径的⊙O与CD相切于点D,点B在⊙O上,连接OB.
(1)求证:DE=OE;
(2)若CD∥AB,求证:BC是⊙O的切线.
【答案】(1)详见解析;(2)详见解析
【解析】
(1)先判断出∠2+∠3=90°,再判断出∠1=∠2即可得出结论;
(2)根据等腰三角形的性质得到∠3=∠COD=∠DEO=60°,根据平行线的性质得到∠4=∠1,根据全等三角形的性质得到∠CBO=∠CDO=90°,于是得到结论;
(1)如图,连接OD,

∵CD是⊙O的切线,
∴OD⊥CD,
∴∠2+∠3=∠1+∠COD=90°,
∵DE=EC,
∴∠1=∠2,
∴∠3=∠COD,
∴DE=OE;
(2)∵OD=OE,
∴OD=DE=OE,
∴∠3=∠COD=∠DEO=60°,
∴∠2=∠1=30°,
∵AB∥CD,
∴∠4=∠1,
∴∠1=∠2=∠4=∠OBA=30°,
∴∠BOC=∠DOC=60°,
在△CDO与△CBO中,
 ,
,
∴△CDO≌△CBO(SAS),
∴∠CBO=∠CDO=90°,
∴OB⊥BC,
∴BC是⊙O的切线;

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
【题目】已知二次函数![]() ,
,![]() 与
与![]() 的部分对应值如下表所示:
的部分对应值如下表所示:
| … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| … | 6 | 1 | -2 | -3 | -2 | m | … |
下面有四个论断:
①抛物线![]() 的顶点为
的顶点为![]() ;
;
②![]() ;
;
③关于![]() 的方程
的方程![]() 的解为
的解为![]() ;
;
④![]() .
.
其中,正确的有___________________