题目内容
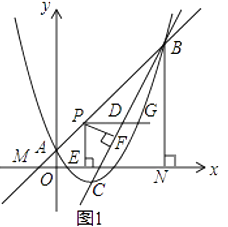
【题目】如图,直线OC、BC的函数关系式分别是y1=x和y2=﹣2x+6,直线BC与x轴交于点B,直线BA与直线OC相交于点A.
(1)当x取何值时y1>y2?
(2)当直线BA平分△BOC的面积时,求点A的坐标.

【答案】(1)当x>2时,y1>y2;(2)A(1,1).
【解析】
(1)首先求出直线y1=x和直线y2=-2x+6的交点坐标,然后根据图象和简单坐标就可以求出x取何值时y1>y2;
(2)由于BA平分△BOC的面积,所以S△AOB=![]() S△OBC,过A作AM⊥OB于M,过C作CN⊥OB于N,然后根据三角形的面积公式可以求出AM,再代入直线y=x中就可以求出点A的坐标.
S△OBC,过A作AM⊥OB于M,过C作CN⊥OB于N,然后根据三角形的面积公式可以求出AM,再代入直线y=x中就可以求出点A的坐标.
(1)依题意得![]() ,
,
∴x=﹣2x+6,
∴x=2,
∴![]() ,
,
∴C(2,2),
∴当x>2时,y1>y2;
(2)如图,过A作AM⊥OB于M,过C作CN⊥OB于N,

∵![]() ,
,
而![]() ,
,
∴![]() ,
,
∴![]() ,
,
把y=1代入y=x中,x=1,
∴A(1,1).

练习册系列答案
相关题目
【题目】某县为了了解2013年初中毕业生毕业后的去向,对部分初三学生进行了抽样调查,就初三学生的四种去向
A.读普通高中; | B.读职业高中 | C.直接进入社会就业; | D.其它)进行数据统计,并绘制了两幅不完整的统计图(a)、(b).请问: |


(1)该县共调查了 名初中毕业生;
(2)将两幅统计图中不完整的部分补充完整;
(3)若该县2013年初三毕业生共有4500人,请估计该县今年的初三毕业生中读普通高中的学生人数.