题目内容
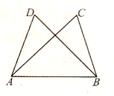
如图,在△ABC中,∠C=90°,AD平分∠CAB,交CB于点D,过点D作DE⊥AB于点E.

(1)求证:△ACD≌△AED;
(2)若∠B=30°,CD=1,求BD的长.

(1)求证:△ACD≌△AED;
(2)若∠B=30°,CD=1,求BD的长.
(1)证明见试题解析;(2)2.
试题分析:(1)根据角平分线性质求出CD=DE,根据HL定理求出另三角形全等即可;
(2)求出∠DEB=90°,DE=1,根据含30度角的直角三角形性质求出即可.
解答:(1)证明:∵AD平分∠CAB,DE⊥AB,∠C=90°,∴CD=ED,∠DEA=∠C=90°,∵在Rt△ACD和Rt△AED中,
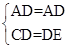 ,∴Rt△ACD≌Rt△AED(HL);
,∴Rt△ACD≌Rt△AED(HL);(2)解:∵DC=DE=1,DE⊥AB,∴∠DEB=90°,∵∠B=30°,∴BD=2DE=2.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
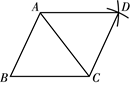

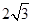 ,则它的边长为( )
,则它的边长为( )
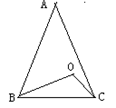
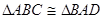 ,AB=6cm,BD=7cm,AD=5cm,则BC的长等于 ( )
,AB=6cm,BD=7cm,AD=5cm,则BC的长等于 ( )