题目内容
如图:AB=AC,∠A=50°,点O是△ABC内一点,且∠OBC=∠ACO,则∠BOC= .
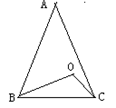

115°
由题, AB=AC,∠A=50°,所以∠ABC=∠ACB, ∠A +∠ABC+∠ACB =180°,故∠ACB=65°,在△BOC中, ∠O +∠OBC+∠OCB =180°,而∠OBC=∠ACO,所以∠O +∠OBC+∠ACO =∠ACB +∠O =180°,∠O=115°.
试题分析:等腰三角形的底角相等,三角形内角和为180°,由题, AB=AC,∠A=50°,所以∠ABC=∠ACB, ∠A +∠ABC+∠ACB =180°,故∠ACB=65°,在△BOC中, ∠O +∠OBC+∠OCB =180°,而∠OBC=∠ACO,所以∠O +∠OBC+∠ACO =∠ACB +∠O =180°,∠O=115°.
试题分析:等腰三角形的底角相等,三角形内角和为180°,由题, AB=AC,∠A=50°,所以∠ABC=∠ACB, ∠A +∠ABC+∠ACB =180°,故∠ACB=65°,在△BOC中, ∠O +∠OBC+∠OCB =180°,而∠OBC=∠ACO,所以∠O +∠OBC+∠ACO =∠ACB +∠O =180°,∠O=115°.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

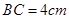 ,
,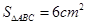 ,求AD和EC的长.
,求AD和EC的长.