��Ŀ����
����Ŀ����ͼ��ʾ��ij���̶�����ɽ�£�ɽ����Ϊֱ��l������һ��·����Ҫ����ɽ�µ��¶ȣ���tan����ֵ������Ա��ɽ��P�������ƴ������ߣ��۲����ɽ���ϵ�һ���������������C������Ϊ31�㣬����B������Ϊ26.6�㣮��֪����BC=40�ף������ڵ�ɽ��OB=240�ף�OA=300�ף�ͼ�еĵ�O��B��C��A��P��ͬһƽ���ڣ�
��
��1��P��OC�ľ��룮
��2��ɽ�µ��¶�tan����
�������sin26.6���0.45��tan26.6���0.50��sin31���0.52��tan37���0.60��
���𰸡�
��1��
�⣺��ͼ������P��PD��OC��D��PE��OA��E�����ı���ODPEΪ���Σ�
��Rt��PBD�У��ߡ�BDP=90�㣬��BPD=26.6�㣬
��BD=PDtan��BPD=PDtan26.6�㣻
��Rt��CPD�У��ߡ�CDP=90�㣬��CPD=31�㣬
��CD=PDtan��CPD=PDtan31�㣻
��CD��BD=BC��
��PDtan31�㩁PDtan26.6��=40��
��0.60PD��0.50PD=40��
���PD=400���ף���
��P��OC�ľ���Ϊ400��
��2��
�⣺��Rt��PBD�У�BD=PDtan26.6���400��0.50=200���ף���
��OB=240�ף�
��PE=OD=OB��BD=40�ף�
��OE=PD=400�ף�
��AE=OE��OA=400��300=100���ף���
��tan��= ![]() =0.4��
=0.4��
���¶�Ϊ0.4��
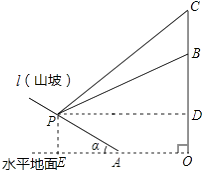
����������1������P��PD��OC��D��PE��OA��E�����ı���ODPEΪ���Σ��Ƚ�Rt��PBD���ó�BD=PDtan26.6�㣻��Rt��CPD���ó�CD=PDtan31�㣻�ٸ���CD��BD=BC���г����̣����PD=400������õ�P��OC�ľ��룻��2��������õ��߶�PD�ij����PE=40��AE=100��Ȼ���ڡ�APE���������Ǻ����Ķ��弴����⣮

 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�