题目内容
已知抛物线y=x2-(m2+5)x+2m2+6.(1)求证:无论m为何值,抛物线与x轴必有两个交点,并且有一个交点必为A(2,0);
(2)设抛物线与x轴的另一个交点为B,记AB的长为d,求d与m之间的函数关系式;
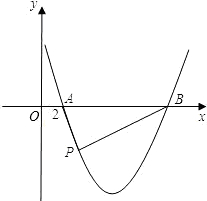
(3)令d=10,问抛物线上是否存在点P,使△ABP为直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
分析:(1)令抛物线中y=0,即可用十字相乘法求得两根的值,由此可得证.
(2)在(1)中已经求得了两点的坐标,即可表示出AB的距离.
(3)根据d的长以及(2)中得出的d的表达式可确定出抛物线的解析式,也就能得出A、B的坐标.可以AB为直径作圆,圆与抛物线有交点,说明抛物线上存在符合条件的P点,可根据抛物线的解析式设出P点坐标(设横坐标,根据抛物线的解析式表示出纵坐标),在直角三角形ABP中,∠APB=90°,如果过P作PQ⊥x轴于Q,那么根据射影定理可得出PQ2=AQ•QB,由此可求出P点坐标.
(2)在(1)中已经求得了两点的坐标,即可表示出AB的距离.
(3)根据d的长以及(2)中得出的d的表达式可确定出抛物线的解析式,也就能得出A、B的坐标.可以AB为直径作圆,圆与抛物线有交点,说明抛物线上存在符合条件的P点,可根据抛物线的解析式设出P点坐标(设横坐标,根据抛物线的解析式表示出纵坐标),在直角三角形ABP中,∠APB=90°,如果过P作PQ⊥x轴于Q,那么根据射影定理可得出PQ2=AQ•QB,由此可求出P点坐标.
解答:解:(1)令y=0,得x2-(m2+5)x+2m2+6=0,
即(x-2)(x-m2-3)=0
解得x1=2,x2=m2+3
∴一定有交点A(2,0),B(m2+3,0)
∴结论得证
(2)∵A(2,0),B(m2+3,0)
∴d=AB=m2+1
(3)d=AB=m2+1=10,
∴y=x2-14x+24
∴A(2,0),B(12,0)
以AB为直径画圆,由图可知与抛物线有两个交点
∴存在这样的点P
设点P坐标为(x,x2-14x+24),作P1Q⊥横轴于Q,则点Q(x,0)
易得△AQP∽△PQB
∴
=
,
∴PQ2=AQ•BQ=(x-2)(12-x)=(x2-14x+24)2
即(x-2)(12-x)=(x-2)2(x-12)2,(x-2)(x-12)≠0,
∴解得x=7±2
∴点P为(7+2
,-1),或(7-2
,-1).

即(x-2)(x-m2-3)=0
解得x1=2,x2=m2+3
∴一定有交点A(2,0),B(m2+3,0)
∴结论得证
(2)∵A(2,0),B(m2+3,0)
∴d=AB=m2+1
(3)d=AB=m2+1=10,
∴y=x2-14x+24
∴A(2,0),B(12,0)
以AB为直径画圆,由图可知与抛物线有两个交点
∴存在这样的点P
设点P坐标为(x,x2-14x+24),作P1Q⊥横轴于Q,则点Q(x,0)
易得△AQP∽△PQB
∴
| AQ |
| QP |
| PQ |
| QB |
∴PQ2=AQ•BQ=(x-2)(12-x)=(x2-14x+24)2
即(x-2)(12-x)=(x-2)2(x-12)2,(x-2)(x-12)≠0,
∴解得x=7±2
| 6 |
∴点P为(7+2
| 6 |
| 6 |
点评:本题考查了二次函数与一元二次方程的关系、直角三角形的判定等知识.综合性较强,难度适中.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
已知抛物线y=x2-8x+c的顶点在x轴上,则c等于( )
| A、4 | B、8 | C、-4 | D、16 |
 (1)求b+c的值;
(1)求b+c的值;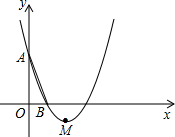 (2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.
(2012•虹口区一模)如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c经过A(0,3),B(1,0)两点,顶点为M.