题目内容
若抛物线y=x2-2x+m的最低点的纵坐标为n，则m-n的值是
- A.-1
- B.0
- C.1
- D.2
C
分析：依据二次函数求最值的纵坐标公式，可得
=
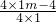=n，进而有m-1=n，于是m-n=1．
解答：∵y=x2-2x+m，
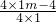∴==n，
即m-1=n，
∴m-n=1．
故选C．
点评：本题考查了二次函数的最值，解题的关键是掌握二次函数的最值公式，并会求最值．
分析：依据二次函数求最值的纵坐标公式，可得
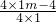==n，进而有m-1=n，于是m-n=1．解答：∵y=x2-2x+m，
∴
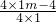==n，即m-1=n，
∴m-n=1．
故选C．
点评：本题考查了二次函数的最值，解题的关键是掌握二次函数的最值公式，并会求最值．
练习册系列答案
阅读快车系列答案
相关题目
若抛物线y=x2-
x-1与x轴有交点，则k的取值范围是（ ）
| k-1 |
| A、k＞-3 | B、k≥-3 |
| C、k≥1 | D、-3≤k≤1 |