题目内容
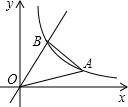 已知,如图A(m,n)是双曲线y=
已知,如图A(m,n)是双曲线y=| k |
| x |
| 3-n |
(1)求k的值;
(2)若点B是直线y=2x与双曲线在第一象限的交点,求点B的坐标;
(3)设点C的坐标为(9,0),点P(x,y)是双曲线y=
| k |
| x |
分析:(1)易得m,n的值,代入双曲线解析式可得k的值;
(2)让正比例函数和双曲线解析式组成方程组,求得在第一象限的交点即可;
(3)易得△AOB的面积,根据它与△POC的面积关系可得到P的纵坐标,进而可得到横坐标.
(2)让正比例函数和双曲线解析式组成方程组,求得在第一象限的交点即可;
(3)易得△AOB的面积,根据它与△POC的面积关系可得到P的纵坐标,进而可得到横坐标.
解答:解:(1)∵|m-6|+
=0,
∴m-6=0,3-n=0,
∴m=6,n=3,
∴k=mn=18;
(2)由题意得:
,
解得x2=9,
∴x=±3,
∵B在第一象限,
∴x=3,
∴y=6,
∴点B的坐标为(3,6);
(3)作AD⊥x轴于点D,作BE⊥x轴于点E.
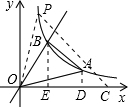 ∵S△AOB=SADEB=
∵S△AOB=SADEB=
(3+6)×3=
;
∵S△POC=
×OC×y=3×
,
∴y=9,
∴x=2,
∴P的坐标为(2,9).
| 3-n |
∴m-6=0,3-n=0,
∴m=6,n=3,
∴k=mn=18;
(2)由题意得:
|
解得x2=9,
∴x=±3,
∵B在第一象限,
∴x=3,
∴y=6,
∴点B的坐标为(3,6);
(3)作AD⊥x轴于点D,作BE⊥x轴于点E.
 ∵S△AOB=SADEB=
∵S△AOB=SADEB=| 1 |
| 2 |
| 27 |
| 2 |
∵S△POC=
| 1 |
| 2 |
| 27 |
| 2 |
∴y=9,
∴x=2,
∴P的坐标为(2,9).
点评:综合考查反比例函数问题;得到△AOB的面积与四边形ADEB的面积关系是解决本题的突破点.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 ,测得C在B的北偏西45°方向上.
,测得C在B的北偏西45°方向上. 11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为
11、已知,如图,正比例函数与反比例函数的图象相交于A、B两点,A点坐标为(2,1),分别以A、B为圆心的圆与x轴相切,则图中两个阴影部分面积的和为 已知,如图,∠1=∠2,
已知,如图,∠1=∠2, 已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为
已知,如图,直角坐标系内的矩形ABCD,顶点A的坐标为(0,3),BC=2AB,P为 于C点,⊙M经过原点O及点A、C,点D是劣弧
于C点,⊙M经过原点O及点A、C,点D是劣弧