题目内容
(本题满分9分)如图所示,△ABC内接于⊙O,AB是⊙O的直径,点D在⊙O
上,过点C的切线交AD的延长线于点E,且AE⊥CE,连接CD.
(1)求证:DC=BC;
(2)若AB=5,AC=4,求tan∠DCE的值.
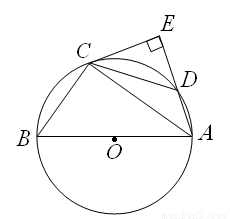
(1)证明:连接OC················································································· 1分

∵OA=OC
∴∠OAC=∠OCA
∵CE是⊙O的切线
∴∠OCE=90° ·············································· 2分
∵AE⊥CE
∴∠AEC=∠OCE=90°
∴OC∥AE ·················································· 3分
∴∠OCA=∠CAD ∴∠CAD=∠BAC
∴
∴DC=BC ··························································································· 4分
(2)∵AB是⊙O的直径 ∴∠ACB=90°
∴ ·························································· 5分
·························································· 5分
∵∠CAE=∠BAC ∠AEC=∠ACB=90°
∴△ACE∽△ABC······················································································ 6分
∴ ∴
∴
 ······················································ 7分
······················································ 7分
∵DC=BC=3
∴ ····················································· 8分
····················································· 8分
∴ -----------9分
(其它解法参考得分)
-----------9分
(其它解法参考得分)
【解析】略

 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案.(本题满分5分)如图一根木棒放在数轴上,木棒的左端与数轴上的点A重合,右端与点B重合.
 |
1.若将木棒沿数轴向右水平移动,则当它的左端移动到B点时,它的右端在数轴上所对应的数为20;若将木棒沿数轴向左水平移动,则当它的右端移动到A点时,则它的左端在数轴上所对应的数为5(单位:cm),由此可得到木棒长为 cm.
2.由题(1)的启发,请你借助“数轴”这个工具帮助小红解决下列问题:
问题:一天,小红去问曾当过数学老师现在退休在家的爷爷的年龄,爷爷说:“我若是你现在这么大,你还要40年才出生;你若是我现在这么大,我已经125岁,是老寿星了,哈哈!”,请求出爷爷现在多少岁了?
 交
交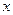 轴于
轴于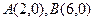 两点,交
两点,交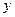 轴于点
轴于点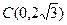 .
.
 (2)若此抛物线的对称轴与直线
(2)若此抛物线的对称轴与直线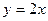 交于点D,作⊙D与x轴相切,⊙D交
交于点D,作⊙D与x轴相切,⊙D交