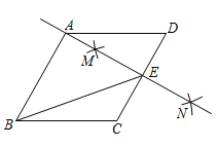
题目内容
【题目】在![]() 中,
中,![]() ,
,![]() ,过点
,过点![]() 作直线
作直线![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转得到
顺时针旋转得到![]() (点
(点![]() 的对应点分别为
的对应点分别为![]() ),射线
),射线![]() 分別交直线
分別交直线![]() 于点
于点![]() .
.
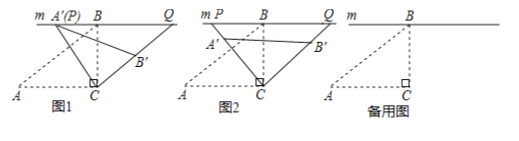
(1)如图,当![]() 与
与![]() 重合时,求
重合时,求![]() 的度数;
的度数;
(2)如图,设![]() 与
与![]() 的交点为
的交点为![]() ,当
,当![]() 为
为![]() 的中点时,求线段
的中点时,求线段![]() 的长;
的长;
(3)在旋转过程中,当点![]() 分别在
分别在![]() 的延长线上时,试探究四边形
的延长线上时,试探究四边形![]() 的面积是否存在最小值.若存在,求出四边形
的面积是否存在最小值.若存在,求出四边形![]() 的最小面积;若不存在,请说明理由.
的最小面积;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ,见解析.
,见解析.
【解析】
1)由旋转可得:AC=A'C=2,进而得到BC=![]() ,依据∠A'BC=90°,可得cos∠A'CB=
,依据∠A'BC=90°,可得cos∠A'CB=![]() ,即可得到∠A'CB=30°,∠ACA'=60°;
,即可得到∠A'CB=30°,∠ACA'=60°;
(2)根据M为A'B'的中点,即可得出∠A=∠A'CM,进而得到PB=![]() ,BC=
,BC=![]() ,依据tan∠Q=tan∠A=
,依据tan∠Q=tan∠A=![]() ,即可得到BQ=BC×
,即可得到BQ=BC×![]() =2,进而得出PQ=PB+BQ=
=2,进而得出PQ=PB+BQ=![]() ;
;
(3)依据S四边形PA'B′Q=S△PCQ-S△A'CB'=S△PCQ-![]() ,即可得到S四边形PA'B′Q最小,即S△PCQ最小,而S△PCQ=
,即可得到S四边形PA'B′Q最小,即S△PCQ最小,而S△PCQ=![]() PQ×BC=
PQ×BC=![]() PQ,利用几何法或代数法即可得到S△PCQ的最小值=3,S四边形PA'B′Q=3-
PQ,利用几何法或代数法即可得到S△PCQ的最小值=3,S四边形PA'B′Q=3-![]() .
.
解:⑴由旋转可得:![]() ,∵
,∵![]() ∴
∴![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ,∴
,∴![]() ;
;
⑵∵![]() 为
为![]() 的中点,∴
的中点,∴![]() ,由旋转可得,
,由旋转可得,![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() ,∵
,∵![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ;
;
⑶∵![]() ,∴
,∴![]() 最小,即
最小,即![]() 最小,
最小,
∴![]() ,取
,取![]() 的中点
的中点![]() ,∵
,∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
当![]() 最小时,
最小时,![]() 最小,∴
最小,∴![]() ,即
,即![]() 与
与![]() 重合时,
重合时,![]() 最小,
最小,
∴![]() ,∴
,∴![]() 的最小值=3,
的最小值=3,![]() ;
;

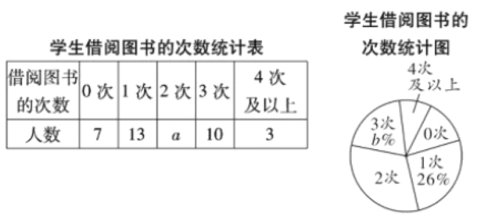
【题目】学校开展“书香校园”活动以来,受到同学们的广泛关注,学校为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如图不完整的统计表.
学生借阅图书的次数:
借阅图书的次数 | 0次 | 1次 | 2次 | 3次 | 4次以上 |
人数 | 7 | 13 |
| 10 | 3 |

请你根据统计图表中的信息,解答下列问题:
(1)![]() ____________,
____________,![]() ____________;
____________;
(2)该调查统计数据的中位数是___________次;
(3)扇形统计图中,“3次”所对应扇形的圆心角的度数是____________;
(4)若该校共有2000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.
【题目】某校八年级学生小丽、小强和小红到某超市参加了社会实践活动,在活动中他们参与了某种水果的销售工作.已知该水果的进价为8元/千克,下面是他们在活动结束后的对话.
小丽:如果以10元/千克的价格销售,那么每天可售出300千克.
小强:如果每千克的利润为3元,那么每天可售出250千克.
小红:如果以13元/千克的价格销售,那么每天可获取利润750元.
【利润=(销售价-进价)![]() 销售量】
销售量】
(1)请根据他们的对话填写下表:
销售单价x(元/kg) | 10 | 11 | 13 |
销售量y(kg) |
(2)请你根据表格中的信息判断每天的销售量y(千克)与销售单价x(元)之间存在怎样的函数关系.并求y(千克)与x(元)(x>0)的函数关系式;
(3)设该超市销售这种水果每天获取的利润为W元,求W与x的函数关系式.当销售单价为何值时,每天可获得的利润最大?最大利润是多少元?