Question

【题目】如图，AB是⊙O的直径，CD是⊙O的一条弦，且CD⊥AB于点E．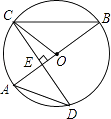

（1）求证：∠BCO=∠D；
（2）若CD= ，AE=2，求⊙O的半径．

Answer 1

【答案】
（1）证明：如图．

∵OC=OB，

∴∠BCO=∠B．

∵∠B=∠D，

∴∠BCO=∠D

（2）解：∵AB是⊙O的直径，且CD⊥AB于点E，

∴CE= CD= ×4 =2 ，

在Rt△OCE中，OC2=CE2+OE2，

设⊙O的半径为r，则OC=r，OE=OA﹣AE=r﹣2，

∴r2=（2 ）2+（r﹣2）2，

解得：r=3，

∴⊙O的半径为3．

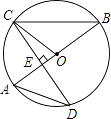
【解析】（1）由OB=OC，利用等边对等角得到一对角相等，再由同弧所对的圆周角相等得到一对角相等，等量代换即可得证；（2）由弦CD与直径AB垂直，利用垂径定理得到E为CD的中点，求出CE的长，在直角三角形OCE中，设圆的半径OC=r，OE=OA﹣AE，表示出OE，利用勾股定理列出关于r的方程，求出方程的解即可得到圆的半径r的值．
【考点精析】掌握勾股定理的概念和垂径定理是解答本题的根本，需要知道直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2；垂径定理：平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧．