��Ŀ����
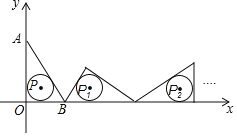
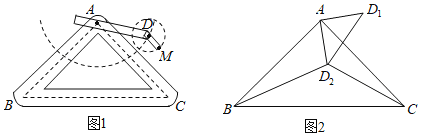
����Ŀ����ͼ����ֱ֪��l��y����1��������L��y��ax2+bx+c��a��0����������L�Ķ���Ϊԭ�㣬�Ҿ�����A(2![]() ,
,![]() )��ֱ��y��kx+1��y�ύ�ڵ�F����������L���ڵ�B��x1��y1����C��x2��y2������x1��x2��
)��ֱ��y��kx+1��y�ύ�ڵ�F����������L���ڵ�B��x1��y1����C��x2��y2������x1��x2��
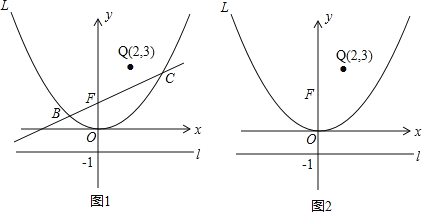
��1����������L�Ľ���ʽ��
��2����P��������L��һ���㣮
���Ե�PΪԲ�ģ�PFΪ�뾶����P�����жϡ�P��ֱ��l��λ�ù�ϵ����˵�����ɣ�
������Q��2��3������|PQ��PF|��ֵ��Сʱ�����P�����ꣻ
��3����֤������kΪ��ֵ��ֱ��l��������BCΪֱ����Բ���У�
���𰸡���1��y��![]() x2����2���ٵ��P��ֱ��l��λ�ù�ϵΪ���У����ɼ��������ڵ�P������Ϊ��2��3������3��������.
x2����2���ٵ��P��ֱ��l��λ�ù�ϵΪ���У����ɼ��������ڵ�P������Ϊ��2��3������3��������.
��������
��1�������ߵı���ʽΪ��y=ax2������A���������ʽ��������⣻
��2���ٵ�F��0��1�����裺��P��m��![]() m2������PF=
m2������PF=![]() m2+1������P��ֱ��l�ľ���Ϊ��
m2+1������P��ֱ��l�ľ���Ϊ��![]() m2+1��������⣻�ڵ���P��Q��F���㹲��ʱ��|PQ-PF|��С��������⣻
m2+1��������⣻�ڵ���P��Q��F���㹲��ʱ��|PQ-PF|��С��������⣻
��3��x2-x1=![]() =4����ֱ��BC����б��Ϊ������tan��=k����cos��=
=4����ֱ��BC����б��Ϊ������tan��=k����cos��=![]() ����BC=
����BC=![]() =4��k2+1������
=4��k2+1������![]() BC=2k2+2����BC���е�ΪM��2k��2k2+1�������M��ֱ��l�ľ���Ϊ��2k2+2��������⣮
BC=2k2+2����BC���е�ΪM��2k��2k2+1�������M��ֱ��l�ľ���Ϊ��2k2+2��������⣮
��1�������ߵı���ʽΪ��y=ax2��
����A���������ʽ�ã�![]() =a��2
=a��2![]() ��2����ã�a=
��2����ã�a=![]() ��
��
�������ߵı���ʽΪ��y=![]() x2�٣�
x2�٣�
��2���ٵ�F��0��1�����裺��P��m��![]() m2����
m2����
��PF=![]() m2+1=
m2+1=![]() m2+1��
m2+1��
����P��ֱ��l�ľ���Ϊ��![]() m2+1��
m2+1��
���P��ֱ��l��λ�ù�ϵΪ���У�
�ڵ���P��Q��F���㹲��ʱ��|PQ-PF|��С��
����FQ���������һ�κ�������ʽ��y=kx+b����ã�
ֱ��FQ�ĺ�������ʽΪ��y=x+1���ڣ�
�����٢ڲ���ã�x=2��
�ʵ�P������Ϊ����2��3����
��3���������ߵı���ʽ��ֱ��y=kx+1�����������ã�
x2-4kx-4=0��
��x1+x2=4k��x1x2=-4��
��y1+y2=k��x1+x2��+2=4k2+2��
��x2-x1=![]() =4��
=4��
��ֱ��BC����б��Ϊ������tan��=k����cos��=![]() ����BC=
����BC=![]() =4��k2+1������
=4��k2+1������![]() BC=2k2+2��
BC=2k2+2��
��BC���е�ΪM��2k��2k2+1�������M��ֱ��l�ľ���Ϊ��2k2+2��
��ֱ��l��������BCΪֱ����Բ���У�

 ���ſ����ϵ�д�
���ſ����ϵ�д� ���Ŀ����ϵ�д�
���Ŀ����ϵ�д� ������ӱ������ͯ������ϵ�д�
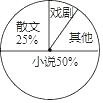
������ӱ������ͯ������ϵ�д�����Ŀ�����꼶һ�չ������һ���������Ļ����ί���ѧ���Ķ��鼮������������ʾ����飬�ʾ���������С˵����Ϸ������ɢ�������������ĸ����ͣ�ÿλͬѧ��ѡһ����ݵ����������˲�������Ƶ���ֲ���������ͳ��ͼ��
��� | Ƶ���������� | Ƶ�� |
С˵ | 0.5 | |
Ϸ�� | 4 | |
ɢ�� | 10 | 0.25 |
���� | 6 | |
�ϼ� | 1 |
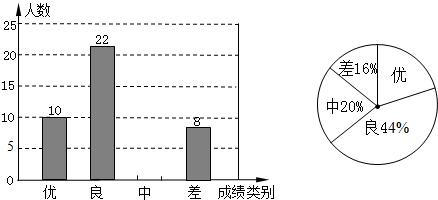
����ͼ���ṩ����Ϣ������������⣺
��1�����꼶һ���ж�����ѧ����
��2���벹ȫƵ���ֲ��������������ͳ��ͼ��������������ռ�İٷֱȣ�
��3���ڵ����ʾ��У��ס��ҡ���������λͬѧѡ������Ϸ�����࣬�ִ�������λͬѧ������ѡ�� 2 ��ͬѧ�μ�ѧУ��Ϸ����ȤС�飬���û���״ͼ���б����ķ�������ѡȡ�� 2 ��ǡ�����Һͱ��ĸ��ʣ�