Question

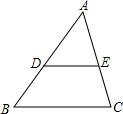如图，若已知△ABC中，D、E分别为AB、AC的中点，则可得DE∥BC，且DE=BC．根据上面的结论：
（1）你能否说出顺次连接任意四边形各边中点，可得到一个什么特殊四边形并说明理由；
（2）如果将（1）中的“任意四边形”改为条件是“平行四边形”或“菱形”或“矩形”或“等腰梯形”，那么它们的结论又分别怎样呢？请说明理由．

Answer 1

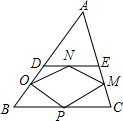解：（1）设四边形DBCE的中点分别为OPMN，则PM=ON，且PM∥ON?顺次连接任意四边形各边中点得到平行四边形；

（2）平行四边形，矩形，菱形，
根据各个四边形的性质：
当四边形为菱形时，连接菱形各边中点所得出的为矩形；
当四边形为矩形时，连接各边中点所得出的为菱形；
当四边形为等腰梯形时，连接各边中点所得为菱形．
分析：设四边形DBCE的中点分别为OPMN，根据已知条件及平行四边形的性质可得到是一个平行四边形；根据各四边的性质进行分析即可．
点评：本题考查的是各个四边形的性质以及等腰梯形的性质的运用．