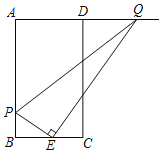
题目内容
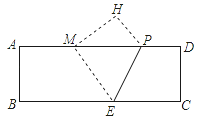
【题目】如图,在矩形ABCD中,![]() ,
,![]() ,点E是边BC的中点
,点E是边BC的中点![]() 动点P从点A出发,沿着AB运动到点B停止,速度为每秒钟1个单位长度,连接PE,过点E作PE的垂线交射线AD与点Q,连接PQ,设点P的运动时间为t秒.
动点P从点A出发,沿着AB运动到点B停止,速度为每秒钟1个单位长度,连接PE,过点E作PE的垂线交射线AD与点Q,连接PQ,设点P的运动时间为t秒.
![]() 当
当![]() 时,
时,![]() ______;
______;
![]() 是否存在这样的t值,使
是否存在这样的t值,使![]() 为等腰直角三角形?若存在,求出相应的t值,若不存在,请说明理由;
为等腰直角三角形?若存在,求出相应的t值,若不存在,请说明理由;
![]() 当t为何值时,
当t为何值时,![]() 的面积等于10?
的面积等于10?
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() ,见解析;(3)
,见解析;(3)![]() .
.
【解析】
(1)由题意得出AP=1,BP=3,BE=CE=1,利用勾股定理求得PE=![]() ,根据正弦函数的定义可得答案;
,根据正弦函数的定义可得答案;
(2)证△BPE∽△CEF得![]() ,据此求得CF=
,据此求得CF=![]() ,DF=
,DF=![]() ,再证△ECF∽△QDF得
,再证△ECF∽△QDF得![]() ,据此求得DQ=15﹣4t,AQ=17﹣4t,根据△APQ为等腰直角三角形列方程求解可得答案;
,据此求得DQ=15﹣4t,AQ=17﹣4t,根据△APQ为等腰直角三角形列方程求解可得答案;
(3)根据S△PEQ=S直角梯形ABEQ﹣S△APQ﹣S△BPE=2t2﹣16t+34及△PEQ的面积等于10列方程求解可得.
解:![]() 根据题意知,当
根据题意知,当![]() 时,
时,![]() ,
,
则![]() ,
,
![]() ,点E是边BC的中点,
,点E是边BC的中点,
![]() ,
,
则![]() ,
,
![]() 在
在![]() 中,
中,![]() ,
,
故答案为:![]() ;
;
![]() 存在,
存在,![]() .
.
如图,记QE与CD的交点为F,

由题意知![]() ,
,![]() ,
,
![]() 四边形ABCD是矩形,
四边形ABCD是矩形,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,即
,即![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ∽
∽![]() ,
,
![]() ,即
,即 ,
,
![]() ,
,
则![]() ,
,
![]() 为等腰直角三角形,
为等腰直角三角形,
![]() ,即
,即![]() ,
,
解得![]() ,
,
故当![]() 时,
时,![]() 为等腰直角三角形.
为等腰直角三角形.

![]() ,
,
由题意知![]() ,
,
解得![]() 或
或![]() ,
,
![]() ,
,
![]() .
.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案【题目】根据扬州市某风景区的旅游信息,![]() 公司组织一批员工到该风景区旅游,支付给旅行社
公司组织一批员工到该风景区旅游,支付给旅行社![]() 元.
元. ![]() 公司参加这次旅游的员工有多少人?
公司参加这次旅游的员工有多少人?
扬州市某风景区旅游信息表
旅游人数 | 收费标准 |
不超过 | 人均收费 |
超过 | 每增加 |
【题目】在一个不透明的口袋里装有颜色不同的黑、白两种颜色的球共4个,某学习小组进行摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再放回,下表是活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 33 | 60 | 130 | 202 | 251 |
摸到黑球的频率 |
|
|
|
|
|
|
![]() 当n很大时,估计从袋中摸出一个黑球的概率是______;
当n很大时,估计从袋中摸出一个黑球的概率是______;
![]() 试估算口袋中白球有______个;
试估算口袋中白球有______个;
![]() 在
在![]() 的条件下,若从中先换出一球,不放回,摇匀后再摸出一球,请用列表或树状图的方法求两次都摸到白球的概率.
的条件下,若从中先换出一球,不放回,摇匀后再摸出一球,请用列表或树状图的方法求两次都摸到白球的概率.