Question

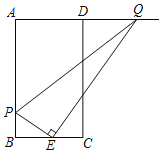
【题目】如图，在每个小正方形的边长为 1 的网格中，点 A、B、C 均在格点上，BC 与网格交于点 P，（1）△ABC 的面积等于______；（2）在 AC 边上有一点 Q，当 PQ 平分△ABC 的面积时，请在如图所示的网格中，用无刻度的直尺，画出 PQ，并简要说明点 Q 的位置是如何找到的(不要求证明)_____________.

Answer 1

【答案】9； 图见解析，选取BC的中点D；选取点F，连接AF与网格交于点E，连接DE（DE与AP平行且相等）与AC交于点Q；连接PQ.

【解析】

（1）利用分割法求得△ABC的面积即可；

（2）根据图中P点的位置可得CD=2BP=2DP，再根据等高的两个三角形的面积比等于底的比，结合已知PQ 平分△ABC 的面积，可得CQ：AC=2：3，然后通过作图找出点Q即可．（方法不唯一）

解：（1）如图

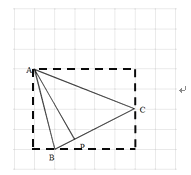
S△ABC

故答案为：9

（2）根据图中P点的位置可得CD=2BP=2DP，设AC 边上有一点 Q，使PQ 平分△ABC 的面积，且设的面积为x，则的面积为2x，

∴的面积为3x，

∵PQ 平分△ABC 的面积，

∴的面积为6x，

∵PC=BC

∴的面积为4.5x；

∴CQ：AC=3x：4.5x=2:3；

方法一：如图，选取BC的中点D；选取点F，连接AF与网格交于点E，连接DE（DE与AP平行且相等）与AC交于点Q；连接PQ,则点Q即为所求．

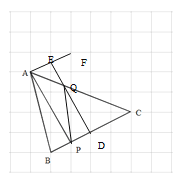
根据题意可得AF//DP,且AE=DP

∴四边形APDE为平行四边形；

∴AP//DQ

∴CQ：AC=CD：CP=2:3；

方法二：如图，选取E、F，连接EF与AC交于点Q，连接PQ则点Q即为所求．

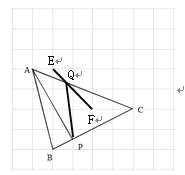
∵AE//CF

∴

∴AQ :CQ =AE:CF=1:2

∴CQ：AC=2:3；