题目内容
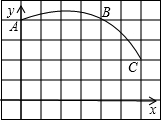 如图,直角坐标系中一条圆弧经过网格点A、B、C,其中B点坐标为(4,4),
如图,直角坐标系中一条圆弧经过网格点A、B、C,其中B点坐标为(4,4),(1)在图上作出该圆弧所在圆的圆心,该圆弧所在圆的圆心坐标为
(2)求出该圆弧所在圆的半径.
分析:(1)可连接AB、BC,分别作弦AB、BC的垂线,根据垂径定理知,弦的垂直平分线经过圆心;则两条弦的垂直平分线的交点必为圆弧所在圆的圆心,然后再判断其坐标即可.
(2)设圆心为M,连接MA,过M作AB的垂线,设垂足为D;根据点M的坐标,可得出MD、AD的长,再由勾股定理即可求出⊙M的半径.
(2)设圆心为M,连接MA,过M作AB的垂线,设垂足为D;根据点M的坐标,可得出MD、AD的长,再由勾股定理即可求出⊙M的半径.
解答:解:(1)该圆弧所在圆的圆心如图所示,该圆弧所在圆的圆心坐标为(2,0)(作图(2分),点坐标2分)(4分)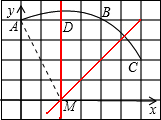
(2)设圆弧所在圆的圆心为M,连接MA;过M作MD⊥AB于D,则MD=4,AD=2;
Rt△MAD中,根据勾股定理,得:
MA=
=2
;
故该圆弧所在圆的半径为2
.(8分)

(2)设圆弧所在圆的圆心为M,连接MA;过M作MD⊥AB于D,则MD=4,AD=2;
Rt△MAD中,根据勾股定理,得:
MA=
| MD2+AD2 |
| 5 |
故该圆弧所在圆的半径为2
| 5 |
点评:此题主要考查的是垂径定理的应用,能够根据垂径定理来确定出圆弧所在圆的圆心,是解答此题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
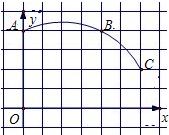 16、如图,直角坐标系中一条圆弧经过网格点A,B,C,其中B点坐标为(4,4),则该圆弧所在圆的圆心坐标为
16、如图,直角坐标系中一条圆弧经过网格点A,B,C,其中B点坐标为(4,4),则该圆弧所在圆的圆心坐标为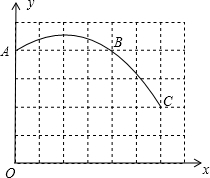 如图,直角坐标系中一条抛物线经过网格点A、B、C,其中B点坐标为(4,4),则该抛物线的关系式
如图,直角坐标系中一条抛物线经过网格点A、B、C,其中B点坐标为(4,4),则该抛物线的关系式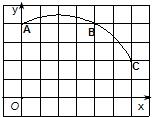 4、如图,直角坐标系中一条圆弧经过网格点A、B、C,其中,B点坐标为(4,4),则该圆弧所在圆的圆心坐标为( )
4、如图,直角坐标系中一条圆弧经过网格点A、B、C,其中,B点坐标为(4,4),则该圆弧所在圆的圆心坐标为( )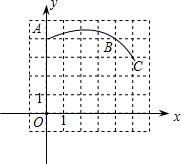 如图,直角坐标系中一条圆弧经过网格点A、B、C,则该圆弧所在圆的圆心坐标为( )
如图,直角坐标系中一条圆弧经过网格点A、B、C,则该圆弧所在圆的圆心坐标为( )