Question

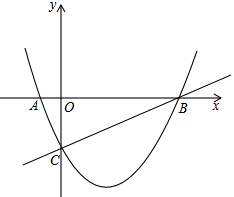
【题目】如图，已知抛物线与x轴相交于A，B两点，并与直线交于B，C两点，其中点C是直线与y轴的交点，连接AC．

（1）求抛物线的解析式；

（2）证明：△ABC为直角三角形；

（3）△ABC内部能否截出面积最大的矩形DEFG？（顶点D、E、F、G在△ABC各边上）若能，求出最大面积；若不能，请说明理由．

Answer 1

【答案】（1） y=x2-x-2．（2）证明见解析；（3）．

【解析】

试题分析：（1）由直线y=x-2交x轴、y轴于B、C两点，则B、C坐标可求．进而代入抛物线y=ax2-x+c，即得a、c的值，从而有抛物线解析式．

（2）求证三角形为直角三角形，我们通常考虑证明一角为90°或勾股定理．本题中未提及特殊角度，而已知A、B、C坐标，即可知AB、AC、BC，则显然可用勾股定理证明．

（3）在直角三角形中截出矩形，面积最大，我们易得两种情形，①一点为C，AB、AC、BC边上各有一点，②AB边上有两点，AC、BC边上各有一点．讨论时可设矩形一边长x，利用三角形相似等性质表示另一边，进而描述面积函数．利用二次函数最值性质可求得最大面积．

试题解析：（1）∵直线y=x-2交x轴、y轴于B、C两点，

∴B（4，0），C（0，-2），

∵y=ax2-x+c过B、C两点，

∴，

解得 ，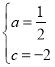

∴y=x2-x-2．

（2）如图1，连接AC，

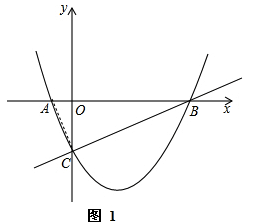
∵y=x2-x-2与x负半轴交于A点，

∴A（-1，0），

在Rt△AOC中，

∵AO=1，OC=2，

∴AC=，

在Rt△BOC中，

∵BO=4，OC=2，

∴BC=2，

∵AB=AO+BO=1+4=5，

∴AB2=AC2+BC2，

∴△ABC为直角三角形．

（3）△ABC内部可截出面积最大的矩形DEFG，面积为，理由如下：

①一点为C，AB、AC、BC边上各有一点，如图2，此时△AGF∽△ACB∽△FEB．

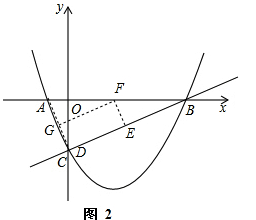
设GC=x，AG=-x，

∵，

∴，

∴GF=2-2x，

∴S=GCGF=x（2-2x）=-2x2+2x=-2[（x-）2-]=-2（x-）2+，

即当x=时，S最大，为．

②AB边上有两点，AC、BC边上各有一点，如图3，此时△CDE∽△CAB∽△GAD，

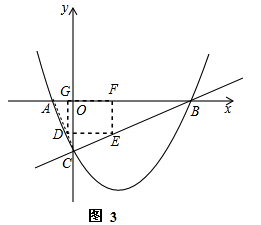
设GD=x，

∵，

∴，

∴AD=x，

∴CD=CA-AD=，

∵，

∴，

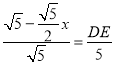∴DE=5-x，

∴S=GDDE=x（5-x）=-x2+5x=-[（x-1）2-1]=-（x-1）2+．

即x=1时，S最大，为．

综上所述，△ABC内部可截出面积最大的矩形DEFG，面积为．