题目内容
一枚质地均匀的正方体骰子的六个面上的数字分别是1，2，2，3，3，4；另一枚质地均匀的正方体骰子的六个面上的数字分别是1，3，4，5，6，8．同时掷这两枚骰子，则其朝上的面两数之和为7的概率是分析：运用列表法直接的出得出所有的可能，然后得出朝上的面两数之和为7的个数，即可求出概率．
解答：解：在36对可能出现的结果中，有6对：（1，6），（2，5），（2，5），（3，4），（3，4），（4，3）的和为7，
所以朝上的面两数字之和为7的概率是
=
．
故答案为：
．
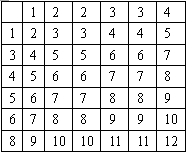
所以朝上的面两数字之和为7的概率是
| 6 |
| 36 |
| 1 |
| 6 |
故答案为：
| 1 |
| 6 |
点评：此题主要考查了用列表法求概率，这种方法能比较直观得出所求数据的所有可能，求概率比较简单．
练习册系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
抛掷一枚质地均匀的正方体骰子，若正面向上点数为2的概率为P（A）；正面向上点数为奇数的概率为P（B）；正面向上点数为7的概率为P（C）．则P（A）、P（B）、P（C）的大小关系是（ ）
| A、P（A）＞P（B）＞P（C） | B、P（C）＞P（A）＞P（B） | C、P（B）＞P（A）＞P（C） | D、P（A）＞P（C）＞P（B） |