题目内容
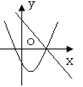
【题目】如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2,9),与y轴交于点A(0,5),与x轴交于点E,B.
(1)求二次函数y=ax2+bx+c的解析式;
(2)过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,线段PD最长?并求出最大值;
(3)若点M在抛物线上,点N在其对称轴上,使得以A,E,N,M为顶点的四边形是平行四边形,求点M的坐标.(请直接写出结果)

【答案】(1)y=﹣x2+4x+5;(2)x=![]() 时,PD的最大值为
时,PD的最大值为![]() ;(3)点M(3,8)或(1,8).
;(3)点M(3,8)或(1,8).
【解析】
(1)设出抛物线解析式,用待定系数法求解即可;
(2)先求出直线AB解析式,设出点P坐标(x,﹣x2+4x+5),建立PD的函数关系式,即可求解;
(3)方法1、先判断出△HMN≌△AOE,求出M点的横坐标,从而求出点M,N的坐标.
方法2、四边形AENM是平行四边形时,由于知道点E和点N的横坐标,进而得出点E平移到点N时,先向右平移3单位,进而判断出点A到点M向右先平移3个单位,求出点M的横坐标,代入抛物线解析式,即可求出点M坐标,判断出点A再向上平移3个单位得出点M,即可求出点N坐标;四边形AEMN是平行四边形时,同上方法即可得出结论
解:(1)设抛物线解析式为y=a(x﹣2)2+9,
∵抛物线与y轴交于点A(0,5),
∴4a+9=5,
∴a=﹣1,
y=﹣(x﹣2)2+9=﹣x2+4x+5,
(2)当y=0时,﹣x2+4x+5=0,
∴x1=﹣1,x2=5,
∴E(﹣1,0),B(5,0),
设直线AB的解析式为y=mx+n,
∵A(0,5),B(5,0),
∴m=﹣1,n=5,
∴直线AB的解析式为y=﹣x+5;
设P(x,﹣x2+4x+5),
∴D(x,﹣x+5),
∴PD=﹣x2+4x+5+x﹣5=﹣x2+5x,
x=![]() 时,PD的最大值为:
时,PD的最大值为:![]() ;
;
(3)方法1、如图,

过M作MH垂直于对称轴,垂足为H,
∵MN∥AE,MN=AE,
∴△HMN≌△AOE,
∴HM=OE=1,
∴M点的横坐标为x=3或x=1,
当x=1时,M点纵坐标为8,
当x=3时,M点纵坐标为8,
∴M点的坐标为M1(1,8)或M2(3,8),
∵A(0,5),E(﹣1,0),
∴直线AE解析式为y=5x+5,
∵MN∥AE,
∴MN的解析式为y=5x+b,
∵点N在抛物线对称轴x=2上,
∴N(2,10+b),
∵AE2=OA2+OE2=26
∵MN=AE
∴MN2=AE2,
∴MN2=(2﹣1)2+[8﹣(10+b)]2=1+(b+2)2
∵M点的坐标为M1(1,8)或M2(3,8),
∴点M1,M2关于抛物线对称轴x=2对称,
∵点N在抛物线对称轴上,
∴M1N=M2N,
∴1+(b+2)2=26,
∴b=3,或b=﹣7,
∴10+b=13或10+b=3
∴当M点的坐标为(1,8)时,N点坐标为(2,13),
当M点的坐标为(3,8)时,N点坐标为(2,3).
方法2,如图2,

∴E(﹣1,0),A(0,5),
∵抛物线的解析式为y=﹣(x﹣2)2+9,
∴抛物线的对称轴为直线x=2,
∴点N的横坐标为2,即:N'(2,0)
①当以点A,E,M,N组成的平行四边形为四边形AENM时,
∵E(﹣1,0),点N的横坐标为2,(N'(2,0)
∴点E到点N向右平移2﹣(﹣1)=3个单位,
∵四边形AENM是平行四边形,
∴点A向右也平移3个单位,
∵A(0,5),
∴M点的横坐标为3,即:M'(3,5),
∵点M在抛物线上,
∴点M的纵坐标为﹣(3﹣2)2+9=8,
∴M(3,8),即:点A再向上平移(8﹣5=3)个单位,
∴点N'再向上平移3个单位,得到点N(2,3),
即:当M点的坐标为(3,8)时,N点坐标为(2,3).
②当以点A,E,M,N组成的平行四边形为四边形AEMN时,
同①的方法得出,当M点的坐标为(1,8)时,N点坐标为(2,13);
综上,点M(3,8)或(1,8).

 同步轻松练习系列答案
同步轻松练习系列答案