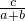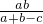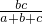Question

某项工程，甲单独需a天完成，在甲做了c（c＜a）天后，剩下工作由乙单独完成还需b天，若开始就由甲乙两人共同合作，则完成任务需（　　）天．

• A、

  c

  a+b

• B、

  ab

  a+b-c

• C、

  a+b-c

  2

• D、

  bc

  a+b+c

Answer 1

分析：等量关系为：（甲的工作效率+乙的工作效率）×甲乙合作的天数=总工作量1，把相关数值代入计算即可．

解答：解：设甲乙合作用x天完成．则乙的工作效率为：（1-甲工作c天的工作量）÷乙的工作天数，
由题意：(

1

a

+

1- c a

b

)x=1，
（

1

a

+

a-c

a

×

1

b

）x=1，

b+a-c

ab

x=1，
解得x=

ab

a+b-c

．故选B．

点评：考查一元一次方程的应用；得到乙的工作效率是解决本题的突破点；得到甲乙合作的工作量的等量关系是解决本题的关键．