题目内容
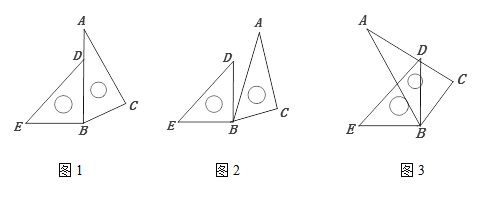
【题目】在等边△ABC中,点E在AB上,点D在CB延长线上,且ED=EC.
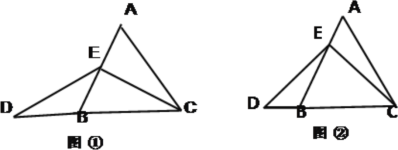
(1)当点E为AB中点时,如图①,AE DB(填“﹥”“﹤”或“=”),并说明理由;
(2)当点E为AB上任意一点时,如图②,AE DB(填“﹥”“﹤”或“=”),并说明理由;(提示:过点E作EF∥BC,交AC于点F)
(3)在等边△ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,请你画出图形,并直接写出相应的CD的长.
【答案】(1)=,理由见解析;(2)=,理由见解析;(3)见解析
【解析】
(1)根据等边三角形性质和等腰三角形的性质求出∠D=∠ECB=30°,求出∠DEB=30°,求出BD=BE即可;
(2)过E作EF∥BC交AC于F,求出等边三角形AEF,证△DEB和△ECF全等,求出BD=EF即可;
(3)当D在CB的延长线上,E在AB的延长线式时,由(2)求出CD=3,当E在BA的延长线上,D在BC的延长线上时,求出CD=1.
解:(1)=,理由如下:
∵ED=EC
∴∠D=∠ECD
∵△ABC是等边三角形
∴∠ACB=∠ABC=60°
∵点E为AB中点
∴∠BCE=∠ACE=30°,AE=BE
∴∠D=30°
∴∠DEB=∠ABC-∠D= 30°
∴∠DEB=∠D
∴BD=BE
∴BD=AE
(2) 过点E作EF∥BC,交AC于点F
∵△ABC是等边三角形
∴∠AEF=∠ABC=60°, ∠AFE=∠ACB=60°, ∠FEC=∠ECB
∴∠EFC=∠EBD=120°
∵ED=EC
∴∠D=∠ECD
∴∠D=∠FEC
在△EFC和 △DBE中

∴△EFC≌△DBE
∴EF=DB
∵∠AEF=∠AFE=60°
∴△AEF 为等边三角形
∴ AE=EF
∴DB =AE
(3)解:CD=1或3,
理由是:分为两种情况:
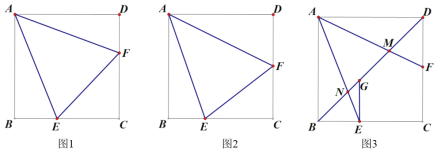
①如图3,过A作AM⊥BC于M,过E作EN⊥BC于N,

则AM∥EN,
∵△ABC是等边三角形,
∴AB=BC=AC=1,
∵AM⊥BC,
∴BM=CM=![]() BC=
BC=![]() ,
,
∵DE=CE,EN⊥BC,
∴CD=2CN,
∵AM∥EN,
∴△AMB∽△ENB,
∴![]() ,
,
∴![]() ,
,
∴BN=![]() ,
,
∴CN=1+![]() =
=![]() ,
,
∴CD=2CN=3;
②如图4,作AM⊥BC于M,过E作EN⊥BC于N,

则AM∥EN,
∵△ABC是等边三角形,
∴AB=BC=AC=1,
∵AM⊥BC,
∴BM=CM=![]() BC=
BC=![]() ,
,
∵DE=CE,EN⊥BC,
∴CD=2CN,
∵AM∥EN,
∴![]() ,
,
∴![]() =
=![]() ,
,
∴MN=1,
∴CN=1-![]() =
=![]() ,
,
∴CD=2CN=1,
即CD=3或1.

【题目】某校七年级为了解课堂发言情况,随机抽取了该年级部分学生,对他们某天在课堂上发言次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知![]() 、
、![]() 两组发言人数的比为
两组发言人数的比为![]() ,请结合图表中相关信息,回答下列问题:
,请结合图表中相关信息,回答下列问题:
组别 | 发言次数 |
|
|
|
|
|
|
|
|
|
|
|
|

(1)求出样本容量,并补全条形统计图;
(2)求![]() 组所在扇形的圆心角的度数;
组所在扇形的圆心角的度数;
(3)该年级共有学生800人,请你估计该年级在这天里发言次数不少于12的人数.