Question

【题目】已知：如图，△ABC中，点D是BC边上的一点，∠ADE=∠ABC=60°，DE交∠ABC的外角平分线于点E．求证：△ADE是等边三角形.

Answer 1

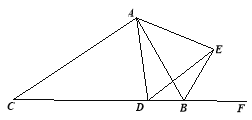
【答案】证明过程见解析

【解析】

试题分析：首先在AB上截取BM=BD，得到△BDM为等边三角形，判定△ADM和△EDB全等，得到AD=DE，根据∠ADE=60°说明△ADE为正三角形.

试题解析：在线段BA上截取BM，使BM=BD． ∵∠ABC=60°

∴△BDM为等边三角形，∠ABF=120°， ∴DM=DB，∠BDM=∠BMD=60°，∠AMD=120°，

又∵BE平分∠ABF， ∴∠DBE=120°， ∴∠AMD=∠DBE，

∵∠ADE =∠BDM =60°， ∴∠1=∠2

∴△ADM≌△EDB（ASA）． ∴AD=ED．

∴△ADE为等边三角形．