题目内容
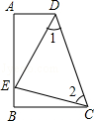
【题目】如图,菱形ABCD中,AB=AC,点E、F分别为边AB、BC上的点,且AE=BF,连接CE、AF交于点H,连接DH交AG于点O.则下列结论①△ABF≌△CAE,②∠AHC=120°,③AH+CH=DH,④AD2=ODDH中,正确的是 .

【答案】①②③④.
【解析】
试题解析:∵四边形ABCD是菱形,
∴AB=BC,
∵AB=AC,
∴AB=BC=AC,
即△ABC是等边三角形,
同理:△ADC是等边三角形
∴∠B=∠EAC=60°,
在△ABF和△CAE中,
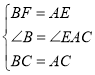 ,
,
∴△ABF≌△CAE(SAS);
故①正确;
∴∠BAF=∠ACE,
∵∠AEH=∠B+∠BCE,
∴∠AHC=∠BAF+∠AEH=∠BAF+∠B+∠BCE=∠B+∠ACE+∠BCE=∠B+∠ACB=60°+60°=120°;
故②正确;
在HD上截取HK=AH,连接AK,
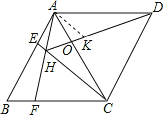
∵∠AHC+∠ADC=120°+60°=180°,
∴点A,H,C,D四点共圆,
∴∠AHD=∠ACD=60°,∠ACH=∠ADH,
∴△AHK是等边三角形,
∴AK=AH,∠AKH=60°,
∴∠AKD=∠AHC=120°,
在△AKD和△AHC中,
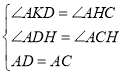 ,
,
∴△AKD≌△AHC(AAS),
∴CH=DK,
∴DH=HK+DK=AH+CH;
故③正确;
∵∠OAD=∠AHD=60°,∠ODA=∠ADH,
∴△OAD∽△AHD,
∴AD:DH=OD:AD,
∴AD2=ODDH.
故④正确.

练习册系列答案
相关题目