Question

【题目】如图，在△ABC中，AD是BC边上的高，∠B=45°，∠C=60°，AD=2，求BC的长．（结果保留根号）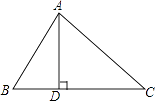

Answer 1

【答案】解：∵AD是BC边上的高，∠C=60°， ∴∠CAD=30°，
∴CD= AC，
在Rt△ACD中，根据勾股定理，
AC2﹣CD2=AD2 ，
（2CD）2﹣CD2=AD2 ，
∴CD= ，
∵AD是BC边上的高，∠B=45°，
∴∠BAD=45°，
∴BD=AD=2，
∴BC=BD+CD=
【解析】分别在RT△ABD和RT△ADC中根据勾股定理和等腰直角三角形的性质求得BD、CD的长，则BC=BD+DC，由此其值就可以得到了．
【考点精析】本题主要考查了勾股定理的概念的相关知识点，需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题．