题目内容
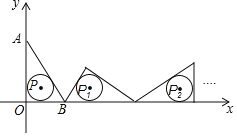
【题目】如图,在平面直角坐标系xOy中,A为x轴上一点,以OA为直径的作半圆M,点B为OA上一点,以OB为边作□OBDC交半圆M于C,D两点.
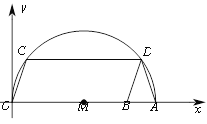
(1)连接AD,求证:DA=DB;
(2)若A点坐标为(20,0),点B的坐标是(16,0),求点C的坐标.
【答案】(1)详见解析;(2)点B的坐标是(2,6)
【解析】
(1)运用平行四边形的性质、四边形的内接圆以及等腰三角形的性质作答即可;
(2) 作DE⊥x轴于点E,延长DC交y轴于点F,连接MD,构造直角三角形,运用勾股定理解答即可.
(1)证明:∵四边形OBDC是平行四边形
∴∠C=∠OBD
∵四边形OADC内接于⊙M
∴∠C+∠A=180°
∵∠OBD+∠ABD=180°
∴∠A=∠ABD
∴DA=DB
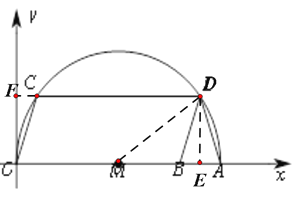
(2)作DE⊥x轴于点E,延长DC交y轴于点F,连接MD,则AE=BE=2,
∴MD=MA=10,ME=8
在Rt△MDE中,由勾股定理可得DE=6
∵BD=OC,CF=DE=6
∴△OCF≌△DBE (HL)
∴CF=BE=2
故点B的坐标是(2,6)

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目