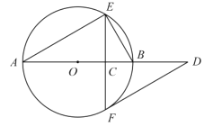
题目内容
【题目】已知等腰直角![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上一点,以
边上一点,以![]() 为边作等腰直角
为边作等腰直角![]() ,其中
,其中![]() ,边
,边![]() 与
与![]() 交于点
交于点![]() ,点
,点![]() 是
是![]() 上一点.
上一点.
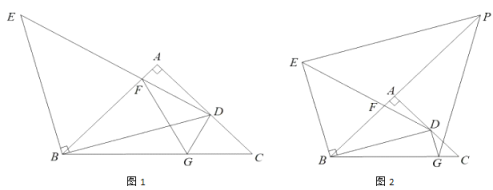
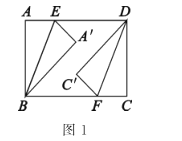
(1)如图1,若![]() ,连接
,连接![]() .
.
①若![]() ,求
,求![]() 的长度;
的长度;
②求证:![]() ;
;
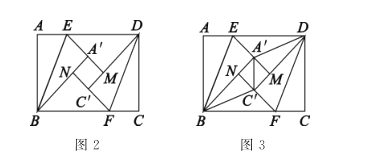
(2)如图2,若![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,请猜想线段
,请猜想线段![]() 之间的数量关系,并证明.
之间的数量关系,并证明.
【答案】(1)①![]() ;②见解析;(2)
;②见解析;(2)![]() .证明见解析.
.证明见解析.
【解析】
(1)①过![]() 作
作![]() 于点
于点![]() ,先由等腰直角
,先由等腰直角![]() 中
中![]() 求得BD的长,设
求得BD的长,设![]() ,分别在Rt△BFM和Rt△DFM中,利用含x的代数式表示出BM和DM的长,再根据
,分别在Rt△BFM和Rt△DFM中,利用含x的代数式表示出BM和DM的长,再根据![]() 求解即可;
求解即可;
②在![]() 上截取
上截取![]() ,连接
,连接![]() ,先证
,先证![]() ,得
,得![]() ,再证
,再证![]() ,得
,得![]() ,进而可证得
,进而可证得![]() ;
;
(2)在![]() 上截取
上截取![]() ,连接
,连接![]() ,先证
,先证![]() ,得
,得![]() ,再证
,再证![]() ,得
,得![]() ,进而可证得
,进而可证得![]() .
.
(1)①如图,过![]() 作
作![]() 于点
于点![]()
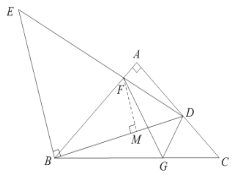
![]() 为等腰直角三角形,
为等腰直角三角形,![]() ,
,
![]() 在
在![]() 中,sin∠E=
中,sin∠E=![]()
∴![]()
设![]() ,
,
在![]() 中,tan∠ABM=
中,tan∠ABM=![]() ,sin∠ABM=
,sin∠ABM=![]() ,
,
∵∠ABM=30°,
∴tan30°=![]() ,sin30°=
,sin30°=![]() ,
,
∴![]()
![]()
同理可得,在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
解得![]() ,
,
![]() ,
,
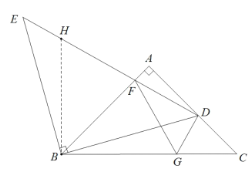
②如图,在![]() 上截取
上截取![]() ,连接
,连接![]()
![]()
![]()
![]() 在
在![]() 与
与![]() 中
中
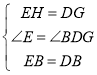
![]()
![]()
![]()
![]()
又![]()
![]()
![]() 在
在![]() 与
与![]() 中
中
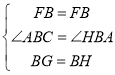
![]()
![]()
![]()
![]()
![]()
(3)如图,在![]() 上截取
上截取![]() ,连接
,连接![]()
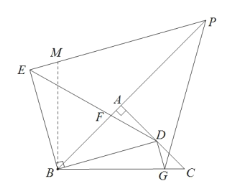
![]()
![]()
![]() 在
在![]() 与
与![]() 中
中
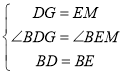
![]()
![]()
![]()
![]()
![]()
![]() 在
在![]() 与
与![]() 中
中
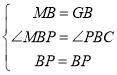
![]()
![]()
![]()
![]()
![]()
![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某超市随机选取1000位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.假定每位顾客购买商品的可能性相同.
商品 顾客人数 | 甲 | 乙 | 丙 | 丁 |
100 | √ | × | √ | √ |
217 | × | √ | × | √ |
200 | √ | √ | √ | × |
300 | √ | × | √ | × |
85 | √ | × | × | × |
98 | × | √ | × | × |
(1)估计顾客同时购买乙和丙的概率为__________.
(2)如果顾客购买了甲,并且同时也在乙、丙、丁中进行了选购,则购买__________(填乙、丙、丁)商品的可能性最大.