Question

【题目】如图，在△ABC中，∠C=90°，以点C为圆心，BC为半径的圆交AB于点D，交AC于点E．

（1）若∠A=25°，求的度数． （2）若BC=9，AC=12，求BD的长．

Answer 1

【答案】(1)弧BD 的度数50°； (2) BD=

【解析】试题分析：（1）求出∠B的度数，求出∠B所对的弧的度数，即可得出答案；

（2）根据勾股定理求出AB，根据割线定理得出比例式，即可得出答案．

试题解析：解：（1）延长BC交⊙O于N，∵在△ABC中，∠C=90°，∠A=25°，∴∠B=65°，∴∠B所对的弧BDN的度数是130°，∴的度数是180°﹣130°=50°；

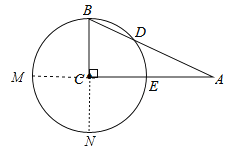
（2）延长AC交⊙O于M，在Rt△BCA中，由勾股定理得：AB= = =15，∵BC=9，AC=12，∴CM=CE=BC=9，AM=AC+CM=21，AE=AC﹣CE=3，由割线定理得：AD×AB=AE×AM，∴（15﹣BD）×15=21×3，解得：BD=．