题目内容
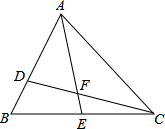
如图所示,△ABC和△ACD都是边长为4厘米等边三角形,两个动点P,Q同时从A点出发,点P以1厘米/秒的速度沿A→C→B的方向运动,点Q以2厘米/秒的速度沿A→B→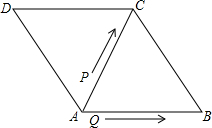 C→D的方向运动,当点Q运动到D点时,P、Q两点同时停止运动.设P、Q运动的时间为t秒时.解答下列问题:
C→D的方向运动,当点Q运动到D点时,P、Q两点同时停止运动.设P、Q运动的时间为t秒时.解答下列问题:
(1)点P、Q从出发到相遇所用时间是______秒;
(2)在P、Q两点运动过程中,当t取何值时,△APQ也是等边三角形?并请说明理由;
(3)当0<t<2时,∠APQ始终是直角,请画出示意图并说明理由.
 C→D的方向运动,当点Q运动到D点时,P、Q两点同时停止运动.设P、Q运动的时间为t秒时.解答下列问题:
C→D的方向运动,当点Q运动到D点时,P、Q两点同时停止运动.设P、Q运动的时间为t秒时.解答下列问题:(1)点P、Q从出发到相遇所用时间是______秒;
(2)在P、Q两点运动过程中,当t取何值时,△APQ也是等边三角形?并请说明理由;
(3)当0<t<2时,∠APQ始终是直角,请画出示意图并说明理由.
(1)设点P、Q从出发到相遇所用时间是t,根据题意得:
t+2t=AC+AB+BC=12,
解得:t=4;
故答案为:4;
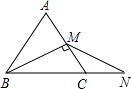
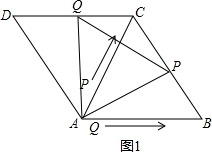
(2)如图1:若△APQ是等边三角形,
此时点P在BC上,点Q在CD上,且△ADQ≌△ACP,
则CP=DQ,即t-4=4-(2t-8),
解得:t=
;
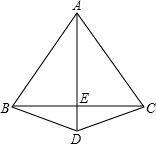
(3)如图2所示:易得:AQ=2AP 又∠PAQ=60度,由对边=斜边一半 得∠AQP=90°,
即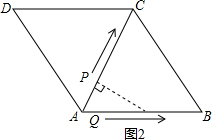 当0<t<2时,∠APQ始终是Rt∠.
当0<t<2时,∠APQ始终是Rt∠.
t+2t=AC+AB+BC=12,
解得:t=4;
故答案为:4;
(2)如图1:若△APQ是等边三角形,
此时点P在BC上,点Q在CD上,且△ADQ≌△ACP,
则CP=DQ,即t-4=4-(2t-8),
解得:t=
| 16 |
| 3 |
(3)如图2所示:易得:AQ=2AP 又∠PAQ=60度,由对边=斜边一半 得∠AQP=90°,
即
 当0<t<2时,∠APQ始终是Rt∠.
当0<t<2时,∠APQ始终是Rt∠.

练习册系列答案
相关题目