题目内容
【题目】已知:AB为⊙O的直径,AB=2,弦DE=1,直线AD与BE相交于点C,弦DE在⊙O上运动且保持长度不变,⊙O的切线DF交BC于点F.
(1)如图1,若DE∥AB,求证:CF=EF;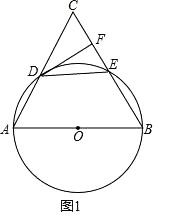
(2)如图2,当点E运动至与点B重合时,试判断CF与BF是否相等,并说明理由.
【答案】
(1)
证明:如图1,连接OD、OE,

∵AB=2,
∴OA=OD=OE=OB=1,
∵DE=1,
∴OD=OE=DE,
∴△ODE是等边三角形,
∴∠ODE=∠OED=60°,
∵DE∥AB,
∴∠AOD=∠ODE=60°,∠EOB=∠OED=60°,
∴△AOD和△△OE是等边三角形,
∴∠OAD=∠OBE=60°,
∴∠CDE=∠OAD=60°,∠CED=∠OBE=60°,
∴△CDE是等边三角形,
∵DF是⊙O的切线,
∴OD⊥DF,
∴∠EDF=90°﹣60°=30°,
∴∠DFE=90°,
∴DF⊥CE,
∴CF=EF
(2)
相等;
如图2,点E运动至与点B重合时,BC是⊙O的切线,

∵⊙O的切线DF交BC于点F,
∴BF=DF,
∴∠BDF=∠DBF,
∵AB是直径,
∴∠ADB=∠BDC=90°,
∴∠FDC=∠C,
∴DF=CF,
∴BF=CF.
【解析】(1)如图1,连接OD、OE,证得△OAD、△ODE、△OEB、△CDE是等边三角形,进一步证得DF⊥CE即可证得结论;(2)根据切线的性质以及等腰三角形的性质即可证得结论.
【考点精析】本题主要考查了切线的性质定理的相关知识点,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径才能正确解答此题.

【题目】青岛市某大酒店豪华间实行淡季、旺季两种价格标准,旺季每间价格比淡季上涨 ![]() .下表是去年该酒店豪华间某两天的相关记录:
.下表是去年该酒店豪华间某两天的相关记录:
淡季 | 旺季 | |
未入住房间数 | 10 | 0 |
日总收入(元) | 24000 | 40000 |
(1)该酒店豪华间有多少间?旺季每间价格为多少元?
(2)今年旺季来临,豪华间的间数不变.经市场调查发现,如果豪华间仍旧实行去年旺季价格,那么每天都客满;如果价格继续上涨,那么每增加25元,每天未入住房间数增加1间.不考虑其他因素,该酒店将豪华间的价格上涨多少元时,豪华间的日总收入最高?最高日总收入是多少元?






