题目内容

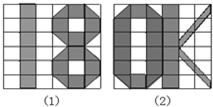已知：图（1）、图（2）分别是6×6正方形网格上两个轴对称图形（阴影部分），其面积分别为SA、SB（网格中最小的正方形面积为一个平方单位），请观察图形并填空：SA：SB的值是
9：11
9：11
．
分析：从网格中数小正方形的个数，进行比较，从图可知，（1）图中有14个小正方形和8个正方形的一半，即有18个正方形．（2）图中有16个小正方形，和12个正方形的一半，即共有22个正方形．由此得出面积比．
解答：解：从图可知：
（1）图中有14个小正方形和8个正方形的一半，即有22个正方形．

（2）图中有16个小正方形，和12个正方形的一半，即共有22个正方形．
由此得出面积比SA：SB=18：22=9：11．
故答案为：9：11．
点评：本题主要考查了图形的面积计算以及网格的实际应用，学生要会利用网格计算面积是解题关键．
练习册系列答案
相关题目
25、（1）①如图1，已知AB∥CD，∠ABC=60°，根据
两直线平行，内错角相等
可得∠BCD=
60
°；
②如图2，在①的条件下，如果CM平分∠BCD，则∠BCM=
30
°；
③如图3，在①、②的条件下，如果CN⊥CM，则∠BCN=
60
°．
（2）尝试解决下面问题：已知如图4，AB∥CD，∠B=40°，CN是∠BCE的平分线，CN⊥CM，求∠BCM的度数．
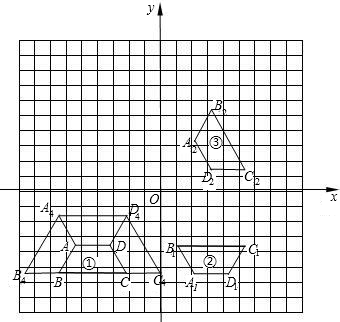如图，在平面直角坐标系中，已知等腰梯形ABCD，AB=AD=DC=2，∠ABC=60°，等腰梯形ABCD称为基本图形，记为图①，现将图①沿AD翻折后平移得到图②；然后将图②以A1为旋转中心，顺时针旋转60°，再向上精英家教网平移8个单位，得到图③；以y轴为对称轴作图③的对称图形，得到等腰梯形A3B3C3D3，即为图④．
（1）画出图④的图形，写出点A、A2、A3的坐标；
（2）将图②、图③、图④通过适当的平移，与图①拼到一起，组成一个新的等腰梯形A4B4C4D4
①在拼成新等腰梯形的过程中，图④经过了怎样的平移？
②对于等腰梯形A4B4C4D4，能否将其中的一个小等腰梯形经过一次图形变换，变成一个平行四边形？如果能，请说明变换过程；如果不能请说明理由．
已知，图23-3-18、图23-3-19分别是6×6正方形网格上的两个轴对称图形(阴影部分)，其面积分别为S1、S2(网格中最小的正方形面积为一个平方单位)，请观察图形并解答下列问题.

　 　　

图23-3-18　　　　　　 图23-3-19　　　　 图23-3-20

(1)求S1∶S2的值.?

(2)请在图23-3-20的网格上画出一个面积为8平方单位的中心对称图形.
　　(黑龙江省2003年中考试题)已知如图1，BD、CE分别是△ABC的外角平分线，过点A作AF⊥BD，AG⊥CE，垂足分别为F、G，连结FG，延长AF、AG，与直线BC相交，易证FG=(AB+BC+AC)．若(1)BD、CE分别是△ABC的内角平分线(如图2)；(2)BD为△ABC的内角平分线，CE为△ABC的外角平分线(如图3)，则在图2，图3两种情况下，线段FG与△ABC三边又有怎样的数量关系？请写出你的猜想，并对其中的一种情况给予证明．

　　猜想结果：图2结论为FG=(AB+AC-BC)．

　　　　 　　　　

图1　　　　　　　　　　　　　图2　　　　　　　　　　　　 图3

 
如图，已知等边△ABC和点P，设点P到△ABC三边AB、AC、BC（或其延长线）的距离分别为h1、h2、h3，△ABC的高为h．
在图1中，点P是边BC的中点，此时h3=0，可得结论：h1+h2+h3=h．
在图2，图3，图4，图5中，点P分别在线段MC上、MC延长线上、△ABC内、△ABC外．
（1）请探究：图2，图3，图4，图5中，h1、h2、h3、h之间的关系；（直接写出结论）
（2）证明图2所得结论；
（3）证明图4所得结论；
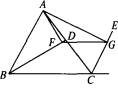
（4）（附加题）在图6中，若四边形RBCS是等腰梯形，∠B=∠C=60°，RS=n，BC=m，点P在梯形内，且点P到四边BR、RS、SC、CB的距离分别是h1、h2、h3、h4，桥形的高为h，则h1、h2、h3、h4、h之间的关系为：h1+h3+h4=．图4与图6中的等式有何关系．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网