Question

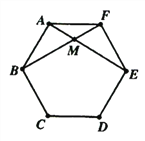
【题目】如图，正六边形ABCDEF的对角线AE与BF相交于点M.

（1）求证：△ABM≌△FEM；

（2）已知AM=2，求BF的长度.

Answer 1

【答案】（1）证明见解析；（2）6

【解析】试题分析：（1）由ASA定理证明△ABM≌△DEN即可；

（2）由30°角所对直角边等于斜边的一半，得到BM的长，再由全等三角形的性质得到AM的长，从而求出BF的长．

试题解析：解：（1）∵六边形ABCDEF是正六边形，∴AB=DE，∠BAF=120°，∴∠ABM=30°，∴∠BAM=90°，同理∠AEF=30°，∠EFM=90°，∴∠ABM=∠AEF，∠BAM=∠EFM，在△ABM和△DEN中，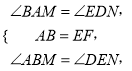

∴△ABM≌△DEN（ASA）．

（2）∵在Rt△ABM中，∠ABM=30°，∴BM=2AM=4．

∵△ABM≌△DEN，∴AM=2，∴BF=BM＋FM=4＋2=6．