题目内容
 (2011•黔东南州)顺次连接一矩形场地ABCD的边AB、BC、CD、DA的中点E、F、G、H,得到四边形EFGH,M为边EH的中点,点P为小明在对角线EG上走动的位置,若AB=10米,BC=10
(2011•黔东南州)顺次连接一矩形场地ABCD的边AB、BC、CD、DA的中点E、F、G、H,得到四边形EFGH,M为边EH的中点,点P为小明在对角线EG上走动的位置,若AB=10米,BC=10| 3 |
10
| ||
| 3 |
10
| ||
| 3 |
分析:由点E、F、G、H分别为矩形ABCD的边AB、BC、CD、DA的中点,得到FH与EG互相垂直平分,则四边形EFGH为菱形,H点与F点关于EG对称,连HF交EG于O点,连FM交EG于P′、连HP′,则P′H=P′F,即P′H+P′M=FM,根据两点之间线段最短得到当动点P运动到点P′的位置时,PM+PH的和为最小值.由AB=10,BC=10
得AE=5,AH=5
,根据勾股定理计算出EH=10,则EM=5,∠AHE=30°,∠EHF=60°,得到△EHF为等边三角形,于是有FM⊥EH,根据含30°的直角三角形三边的关系得到MP′=
EM=
,EP′=2MP′=
,由此得到答案.
| 3 |
| 3 |
| ||
| 3 |
5
| ||
| 3 |
10
| ||
| 3 |
解答:解:∵点E、F、G、H分别为矩形ABCD的边AB、BC、CD、DA的中点,
∴FH与EG互相垂直平分,
∴四边形EFGH为菱形,H点与F点关于EG对称,
连HF交EG于O点,连FM交EG于P′、连HP′,如图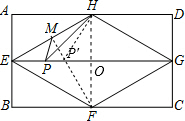 ,
,
则P′H=P′F,即P′H+P′M=FM,
∴当动点P运动到点P′的位置时,PM+PH的和为最小值.
∵AB=10,BC=10
,
∴AE=5,AH=5
,
∴EH=
=10,
∴∠AHE=30°,
∴∠EHF=60°,
∴△EHF为等边三角形,
而M为EH的中点,
∴FM⊥EH,EM=5,
在Rt△EMP′中,∠MEP′=30°,
∴MP′=
EM=
,
∴EP′=2MP′=
,
∴当PM+PH的和为最小值时,EP的长为
m.
故答案为
m.
∴FH与EG互相垂直平分,
∴四边形EFGH为菱形,H点与F点关于EG对称,
连HF交EG于O点,连FM交EG于P′、连HP′,如图
 ,
,则P′H=P′F,即P′H+P′M=FM,
∴当动点P运动到点P′的位置时,PM+PH的和为最小值.
∵AB=10,BC=10
| 3 |
∴AE=5,AH=5
| 3 |
∴EH=
(5
|
∴∠AHE=30°,
∴∠EHF=60°,
∴△EHF为等边三角形,
而M为EH的中点,
∴FM⊥EH,EM=5,
在Rt△EMP′中,∠MEP′=30°,
∴MP′=
| ||
| 3 |
5
| ||
| 3 |
∴EP′=2MP′=
10
| ||
| 3 |
∴当PM+PH的和为最小值时,EP的长为
10
| ||
| 3 |
故答案为
10
| ||
| 3 |
点评:本题考查了轴对称-最短路线问题:通过对称,把两条线段的和转化为一条线段,利用两点之间线段最短解决.也考查了含30°的直角三角形三边的关系、菱形得性质与判定以及矩形的性质.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
 (2011•黔东南州)用若干个大小相同、棱长为1的小正方体搭成一个几何体模型,其三视图如图所示,则搭成这个几何体模型所用的小正方体的个数是( )
(2011•黔东南州)用若干个大小相同、棱长为1的小正方体搭成一个几何体模型,其三视图如图所示,则搭成这个几何体模型所用的小正方体的个数是( )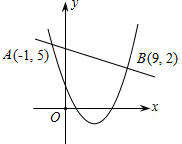 (2011•黔东南州)如图,一次函数y1=kx+n(k≠0)与二次函数y2=ax2+bx+c(a≠0)的图象相交于A(-1,5)、B(9,2)两点,则关于x的不等式kx+n≥ax2+bx+c的解集为( )
(2011•黔东南州)如图,一次函数y1=kx+n(k≠0)与二次函数y2=ax2+bx+c(a≠0)的图象相交于A(-1,5)、B(9,2)两点,则关于x的不等式kx+n≥ax2+bx+c的解集为( )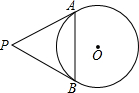 (2011•黔东南州)如图,PA、PB是⊙O的切线,切点分别为A、B,已知⊙O的半径为2,∠P=60°,则弦AB的长为
(2011•黔东南州)如图,PA、PB是⊙O的切线,切点分别为A、B,已知⊙O的半径为2,∠P=60°,则弦AB的长为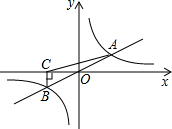 (2011•黔东南州)如图所示,反比例函数
(2011•黔东南州)如图所示,反比例函数