题目内容

13、若a≠b，且a＜0，b＜0，则a3+b3与a2b+ab2比较大小的结果是（　　）
分析：运用求差法和因式分解的方法进行判断差的正负，从而比较大小．
解答：解：∵a＜0，b＜0，
∴a+b＜0，
∴a3+b3-（a2b+ab2）
=（a+b）（a2-ab+b2）-ab（a+b）
=（a+b）（a-b）2＜0
∴a3+b3＜a2b+ab2．
故选B．
点评：此题考查了因式分解的应用，能够熟练运用立方差公式、完全平方公式和提公因式法．
练习册系列答案
相关题目
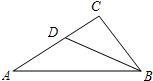精英家教网如图，在△ABC中，AC＞BC，D是AC边上一点，连接BD．
（1）要使△CBD∽△CAB，还需要补充一个条件是
 
；（只要求填一个）
（2）若△CBD∽△CAB，且AD=2，BC=
3
，求CD的长．
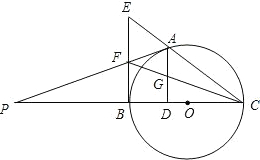如图，A是以BC为直径的⊙O上一点，于点D，AD⊥BC过点B作⊙O的切线精英家教网，与CA的延长线相交于点E，G是AD的中点，连接CG并延长与BE相交于点F，延长AF与CB的延长线相交于点P．
（1）求证：BF=EF；
（2）求证：PA是⊙O的切线；
（3）若FG=BF，且⊙O的半径长为3
2
，求BD和FG的长度．
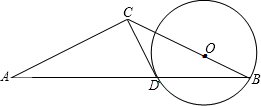如图，△ABC中，AC=BC，以BC上一点O为圆心，OB为半径作⊙O交AB于点精英家教网D．已知经过点D的⊙O切线恰好经过点C．
（1）试判断CD与AC的位置关系，并证明；
（2）若△ACB∽△CDB，且AC=4，求CD的长．
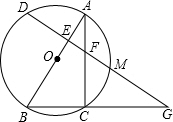精英家教网如图，AB是△ABC的外接圆⊙O的直径，D是⊙O上的一点，DE⊥AB于点E，且DE的延长线分别交AC、⊙O、BC的延长线于F、M、G．
（1）求证：AE•BE=EF•EG；
（2）连接BD，若BD⊥BC，且EF=MF=2，求AE和MG的长．
（2012•嘉定区二模）如图，已知梯形ABCD中，AB∥CD，AB=13，CD=4，点E在边AB上，DE∥BC．
（1）若CE=CB，且tan∠B=3，求△ADE的面积；
（2）若∠DEC=∠A，求边BC的长度．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网