Question

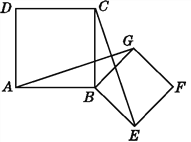
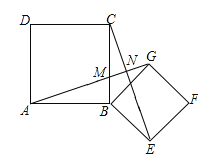
【题目】如图,四边形ABCD,四边形BEFG均为正方形,连接AG,CE.试说明:

(1)AG=CE;

(2)AG⊥CE.

Answer 1

【答案】(1)答案见解析;(2)答案见解析

【解析】试题分析：（1）由正方形的性质有AB=CB，∠ABC=∠GBE=90°，BG=BE，进而得出∠ABG=∠CBE，由SAS证明△ABG≌△CBE，得出对应边相等即可；

（2）由△ABG≌△CBE，得出对应角相等∠BAG=∠BCE，由∠BAG+∠AMB=90°，对顶角∠AMB=∠CMN，得出∠BCE+∠CMN=90°，证出∠CNM=90°即可．

试题解析：证明：（1）∵四边形ABCD、BEFG均为正方形，∴AB=CB，∠ABC=∠GBE=90°，BG=BE，∴∠ABG=∠CBE．

在△ABG和△CBE中，∵AB＝CB，∠ABG＝∠CBE，BG＝BE，∴△ABG≌△CBE（SAS），∴AG=CE；

（2）如图所示：∵△ABG≌△CBE，∴∠BAG=∠BCE．

∵∠ABC=90°，∴∠BAG+∠AMB=90°．

∵∠AMB=∠CMN，∴∠BCE+∠CMN=90°，∴∠CNM=90°，∴AG⊥CE．