题目内容
【题目】已知![]() 的内切圆
的内切圆![]() 与
与![]() 分别相切于点
分别相切于点![]() ,若
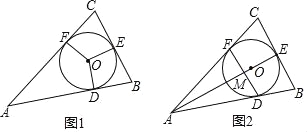
,若![]() ,如图1.
,如图1.
(1)判断![]() 的形状,并证明你的结论;
的形状,并证明你的结论;
(2)设![]() 与
与![]() 相交于点
相交于点![]() ,如图2,
,如图2,![]() 求
求![]() 的长.
的长.
【答案】(1)△ABC为等腰三角形,证明见解析;(2)AM=![]() .
.
【解析】
试题分析:(1)易证∠EOF+∠C=180°,∠DOE+∠B=180°和∠EOF=∠DOE,即可解题;
(2)连接OB、OC、OD、OF,易证AD=AF,BD=CF可得DF∥BC,再根据AE长度即可解题.
试题解析:(1)△ABC为等腰三角形,
∵△ABC的内切圆⊙O与AB、BC、AC分别相切于点D、E、F,∴∠CFE=∠CEF=∠BDO=∠BEO=90°,
∵四边形内角和为360°,∴∠EOF+∠C=180°,∠DOE+∠B=180°,
∵![]() ,∴∠EOF=∠DOE,∴∠B=∠C,AB=AC,∴△ABC为等腰三角形;
,∴∠EOF=∠DOE,∴∠B=∠C,AB=AC,∴△ABC为等腰三角形;
(2)连接OB、OC、OD、OF,如图,
∵等腰三角形ABC中,AE⊥BC,∴E是BC中点,BE=CE,
∵在Rt△AOF和Rt△AOD中![]() ,∴Rt△AOF≌Rt△AOD,∴AF=AD,
,∴Rt△AOF≌Rt△AOD,∴AF=AD,
同理Rt△COF≌Rt△COE,CF=CE=2,Rt△BOD≌Rt△BOE,BD=BE,∴AD=AF,BD=CF,
∴DF∥BC,∴![]() ,
,
∵AE=![]() =4
=4![]() ,∴AM=4
,∴AM=4![]() ×
×![]() =
=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】下表是某报纸公布的我国“九五”期间国内生产总值(GDP)的统计表,那么这几年间我国国内生产总值平均每年比上一年增长___万亿元.
年份 | 1996 | 1997 | 1998 | 1999 | 2000 |
GDP/万亿元 | 6.6 | 7.3 | 7.9 | 8.2 | 8.9 |