题目内容
如图，P是正方形ABCD内一点，连接PA、PB、PC，将△ABP绕点B顺时针旋转到△CBP′的位置．
（1）旋转中心是点 ，旋转的度数是 度；
（2）连结PP′，△BPP′的形状是 三角形；
（3）若PB＝4，求△BPP′的周长。
（1）旋转中心是点 ，旋转的度数是 度；
（2）连结PP′，△BPP′的形状是 三角形；
（3）若PB＝4，求△BPP′的周长。
（1）B 90 （2）等腰直角 （3）8+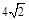
.
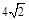.试题分析：（1）P是正方形ABCD内一点，连接PA、PB、PC，将△ABP绕点B顺时针旋转到△CBP′的位置．旋转中心是点B，旋转角是∠ABC,旋转角的度数是90度.
（2）连结PP′,
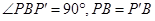,所以△BPP′是等腰直角三角形；（3）若PB＝4，根据勾股定理得:
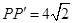,所以△BPP′的周长为4+4+
=8+.试题解析：（1）旋转中心是点B，旋转角是∠ABC,旋转角的度数是90度.
（2）连结PP′,
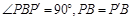,所以△BPP′是等腰直角三角形；（3）若PB＝4，根据勾股定理得:
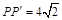,所以△BPP′的周长为4+4+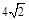=8+.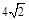
练习册系列答案
第1卷单元月考期中期末系列答案
相关题目
]得△AB′C′，则S△AB′C′：S△ABC=____；直线BC与直线B′C′所夹的锐角为______度；
的正方形
绕它的顶点
旋转
，顶点
所经过的路线长为（ ）
.