题目内容
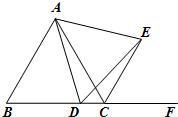 23、如图,△ABC为等边三角形,D为BC上一点,∠ADE=60°,DE交∠ACB外角平分线于E.
23、如图,△ABC为等边三角形,D为BC上一点,∠ADE=60°,DE交∠ACB外角平分线于E.(1)AB与CE平行吗?请说明理由.
(2)请说明∠BAD=∠EDC的理由.
分析:(1)等边三角形各内角为60°,即可求得∠ECF=60°,∵∠ABC=60°,∴AB∥CE;
(2)根据∠BAD+∠ADB=120°,∠ADB+∠EDC=120°,即可求得∠BAD=∠EDC.
(2)根据∠BAD+∠ADB=120°,∠ADB+∠EDC=120°,即可求得∠BAD=∠EDC.
解答:解:(1)∵等边三角形各内角为60°
∴∠ACF=180°-60°=120°,CE为∠ACF的角平分线,
∴∠ECF=60°,∵∠ABC=60°
∴EC∥AB.
(2)∵∠EDC+∠ADE+∠ADB=180°,∴∠EDC+∠ADB=120°,
∵∠ABD+∠BAD+∠ADB=180°,∴∠BAD+∠ADB=120°,
∴∠BAD=∠EDC.
∴∠ACF=180°-60°=120°,CE为∠ACF的角平分线,
∴∠ECF=60°,∵∠ABC=60°
∴EC∥AB.
(2)∵∠EDC+∠ADE+∠ADB=180°,∴∠EDC+∠ADB=120°,
∵∠ABD+∠BAD+∠ADB=180°,∴∠BAD+∠ADB=120°,
∴∠BAD=∠EDC.
点评:本题考查了等边三角形各边长相等、各内角为60°的性质,考查了角平分线的性质,考查了平行线的判定,本题中求得∠EDC+∠ADB=120°,∠BAD+∠ADB=120°是解题的关键.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
相关题目
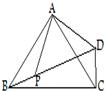 16、如图,△ABC为等边三角形,P为三角形内一点,将△ABP绕A点逆时针旋转60°后与△ACP′重合,若AP=3,则PP′=
16、如图,△ABC为等边三角形,P为三角形内一点,将△ABP绕A点逆时针旋转60°后与△ACP′重合,若AP=3,则PP′=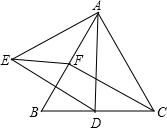 如图,△ABC为等边三角形,D、F分别为BC、AB上的点,且CD=BF,以AD为边作等边△ADE.
如图,△ABC为等边三角形,D、F分别为BC、AB上的点,且CD=BF,以AD为边作等边△ADE. 如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD与Q,PQ=4,PE=1
如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD与Q,PQ=4,PE=1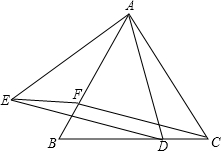 如图,△ABC为等边三角形,D、F分别为CB、BA上的点,且CD=BF,以AD为一边作等边三角形ADE.
如图,△ABC为等边三角形,D、F分别为CB、BA上的点,且CD=BF,以AD为一边作等边三角形ADE. 如图,△ABC为等边△,EC=ED,∠CED=120゜,P为BD的中点,求证:AE=2PE.
如图,△ABC为等边△,EC=ED,∠CED=120゜,P为BD的中点,求证:AE=2PE.