题目内容
 如图,△ABC为等边三角形,D、F分别为CB、BA上的点,且CD=BF,以AD为一边作等边三角形ADE.
如图,△ABC为等边三角形,D、F分别为CB、BA上的点,且CD=BF,以AD为一边作等边三角形ADE.①△ACD与△CBF是全等三角形吗?说说你的理由.
②ED=FC吗?说说你的理由.
分析:①根据等边三角形的性质得出AC=CB,∠ACD=∠CBF=60°,进而利用SAS得出即可;
②由①中的全等三角形的对应边相等推知:FC=DA;然后由等边△ADE的性质得到ED=AD,则根据等量代换可以证得结论.
②由①中的全等三角形的对应边相等推知:FC=DA;然后由等边△ADE的性质得到ED=AD,则根据等量代换可以证得结论.
解答:解:①△ACD与△CBF是全等三角形.理由如下:
∵△ABC为等边三角形,
∴AC=CB,∠ACD=∠CBF=60°,
在△ACD和△CBF中,
,
∴△ACD≌△CBF(SAS);
②ED=FC.理由如下:
由①知:△ACD≌△CBF,则FC=DA.
∵△ADE是等边三角形,
∴ED=AD,
∴ED=FC.
∵△ABC为等边三角形,
∴AC=CB,∠ACD=∠CBF=60°,
在△ACD和△CBF中,
|
∴△ACD≌△CBF(SAS);
②ED=FC.理由如下:
由①知:△ACD≌△CBF,则FC=DA.
∵△ADE是等边三角形,
∴ED=AD,
∴ED=FC.
点评:此题主要考查了全等三角形的判定与性质,等边三角形的性质.全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
 16、如图,△ABC为等边三角形,P为三角形内一点,将△ABP绕A点逆时针旋转60°后与△ACP′重合,若AP=3,则PP′=
16、如图,△ABC为等边三角形,P为三角形内一点,将△ABP绕A点逆时针旋转60°后与△ACP′重合,若AP=3,则PP′=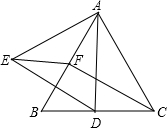 如图,△ABC为等边三角形,D、F分别为BC、AB上的点,且CD=BF,以AD为边作等边△ADE.
如图,△ABC为等边三角形,D、F分别为BC、AB上的点,且CD=BF,以AD为边作等边△ADE. 如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD与Q,PQ=4,PE=1
如图,△ABC为等边三角形,AE=CD,AD、BE相交于点P,BQ⊥AD与Q,PQ=4,PE=1 如图,△ABC为等边△,EC=ED,∠CED=120゜,P为BD的中点,求证:AE=2PE.
如图,△ABC为等边△,EC=ED,∠CED=120゜,P为BD的中点,求证:AE=2PE.