题目内容
如图,直线AB,CD相交于点O,OM⊥AB,垂足为O,若∠1=∠2=30°,求∠NOD.
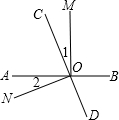

∵OM⊥AB,
∴∠AOM=90°,
∵∠1=30°,
∴∠AOC=60°,
∵∠BOD=∠AOC,
∴∠BOD=60°,
∵∠2+∠NOD+∠BOD=180°,
∴∠NOD=180°-30°-60°=90°.
∴∠AOM=90°,
∵∠1=30°,
∴∠AOC=60°,
∵∠BOD=∠AOC,
∴∠BOD=60°,
∵∠2+∠NOD+∠BOD=180°,
∴∠NOD=180°-30°-60°=90°.

练习册系列答案
相关题目