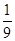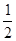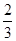题目内容
在一个不透明的盒子中,放入2个白球和1个红球,这些球除颜色外都相同.
(1)搅匀后从中任意摸出2个球,请通过列表或树状图求摸出2个球都是白球的概率;
(2)搅匀后从中任意摸出1个球,记录下颜色后放回袋中,再次搅匀后从中任意摸出1个球,请通过列表或树状图求2次摸出的球都是白球的概率;
(3)现有一个可以自由转动的转盘,转盘被等分成60个相等的扇形,这些扇形除颜色外完全相同,其中40个扇形涂上白色,20个扇形涂上红色,转动转盘2次,指针2次都指向白色区域的概率为 .
(1)搅匀后从中任意摸出2个球,请通过列表或树状图求摸出2个球都是白球的概率;
(2)搅匀后从中任意摸出1个球,记录下颜色后放回袋中,再次搅匀后从中任意摸出1个球,请通过列表或树状图求2次摸出的球都是白球的概率;
(3)现有一个可以自由转动的转盘,转盘被等分成60个相等的扇形,这些扇形除颜色外完全相同,其中40个扇形涂上白色,20个扇形涂上红色,转动转盘2次,指针2次都指向白色区域的概率为 .
试题分析:(1)
| | 白球2个 | 红球1个 |
| 任意摸出2个球 | 2白 | 0红 |
| 1白 | 1红 | |
| 1白 | 1红 |
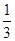 .
. | | 2个白球、一个红球 | ||||||
| 第一次摸球 | 白 | 白 | 红球 | ||||
| 第二次摸球 | 白 | 白 | 红 | 红 | 白 | 白 | |
所以P(2次摸出的球都是白球)=
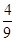
(3)第一次指向白球区域的概率=
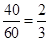 ;第二次指向白球区域的概率=
;第二次指向白球区域的概率= 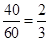
指针2次都指向白色区域的概率=
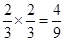
点评:本题考查概率的知识,掌握求事件的概率是解本题的方法

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
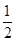

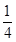
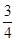
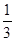 B.
B.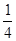 C.
C.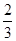 D.
D.