题目内容
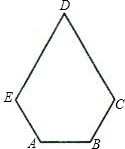 如图,凸五边形ABCDE中,∠A=∠B=120°,EA=AB=BC=2,CD=DE=4,则它的面积为
如图,凸五边形ABCDE中,∠A=∠B=120°,EA=AB=BC=2,CD=DE=4,则它的面积为分析:作辅助线延长EA,BC相交于点F,CG⊥EF于G,BH⊥EF于H,因为∠EAB=∠CBA=120°,可得∠FAB=∠FBA=60°,可得△FAB为等边三角形,容易证明四边形EFCD是菱形,所以SABCDE=SCDEF-S△ABF由此即可求解.
解答: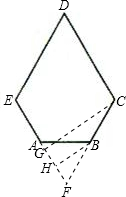 解:如图,延长EA,BC相交于点F,CG⊥EF于G,BH⊥EF于H,
解:如图,延长EA,BC相交于点F,CG⊥EF于G,BH⊥EF于H,
因为∠EAB=∠CBA=120°,
所以∠FAB=∠FBA=60°,
所以△FAB为等边三角形,
AF=FB=AB=2,
所以CD=DE=EF=FC=4,
所以四边形EFCD是菱形,
所以SABCDE=SCDEF-S△ABF
 解:如图,延长EA,BC相交于点F,CG⊥EF于G,BH⊥EF于H,
解:如图,延长EA,BC相交于点F,CG⊥EF于G,BH⊥EF于H,因为∠EAB=∠CBA=120°,
所以∠FAB=∠FBA=60°,
所以△FAB为等边三角形,
AF=FB=AB=2,
所以CD=DE=EF=FC=4,
所以四边形EFCD是菱形,
所以SABCDE=SCDEF-S△ABF
|
点评:本题考查轴对称的性质,对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
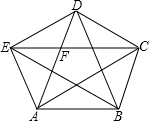 如图,凸五边形ABCDE中,已知S△ABC=1,且EC∥AB,AD∥BC,BE∥CD,CA∥DE,DB∥EA.试求五边形ABCDE的面积.
如图,凸五边形ABCDE中,已知S△ABC=1,且EC∥AB,AD∥BC,BE∥CD,CA∥DE,DB∥EA.试求五边形ABCDE的面积.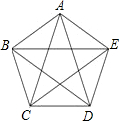 已知:如图,凸五边形ABCDE中,S△ABC=S△BCD=S△CDE=S△DEA=S△EAB=1,则S五边形ABCDE=
已知:如图,凸五边形ABCDE中,S△ABC=S△BCD=S△CDE=S△DEA=S△EAB=1,则S五边形ABCDE=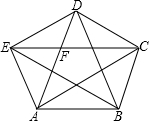 如图,凸五边形ABCDE中,已知S△ABC=1,且EC∥AB,AD∥BC,BE∥CD,CA∥DE,DB∥EA.试求五边形ABCDE的面积.
如图,凸五边形ABCDE中,已知S△ABC=1,且EC∥AB,AD∥BC,BE∥CD,CA∥DE,DB∥EA.试求五边形ABCDE的面积.