Question

（2013•安庆二模）2013年5月31日是第26个“世界无烟日”，校学生会书记小明同学就“戒烟方式”的了解程度对本校九年级学生进行了一次随机问卷调查，如图是他采集数据后绘制的两幅不完整的统计图（A：了解较多，B：不了解，C：了解一点，D：非常了解）．请你根据图中提供的信息解答以下问题：
（1）在扇形统计图中的横线上填写缺失的数据，并把条形统计图补充完整．
（2）2013年该初中九年级共有学生400人，按此调查，可以估计2013年该初中九年级学生中对戒烟方式“了解较多”以上的学生约有多少人？
（3）在问卷调查中，选择“A”的是1名男生，1名女生，选择“D”的有4人且有2男2女．校学生会要从选择“A、D”的问卷中，分别抽一名学生参加活动，请你用列表法或树状图求出恰好是一名男生一名女生的概率．

Answer 1

分析：（1）由条形统计图中A对应的数据和扇形统计图中A对应的百分比可知抽取样本的容量，进而求出选B、D的人数，求出C、D所占的百分比；
（2）找出“了解较多”与“非常了解”的总人数除以样本的容量，再乘以400即可求出结果；
（3）选“A”的是一男一女，记作男1、女1，根据题意可知：选择“D”的有4人且有2男2女，分别记作男2、男3、女2、女3，列出相应的表格，找出所有等可能的情况数，找出一男一女的情况数，即可求出所求的概率．

解答：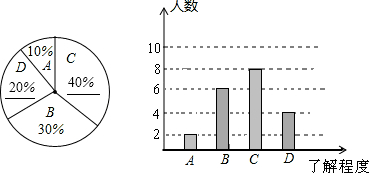
解：（1）由题意得：抽取的样本容量为2÷10%=20，
则选B的有20×30%=6（人）；选D的有20-2-6-8=4（人）；C占8÷20=0.4=40%，D占4÷20=20%，
补全统计图，如图所示；                   
（2）∵选项“了解较多”以上的学生占抽取样本容量的：（2+4）÷20=30%，
则M初中九年级学生中对羽毛球知识“了解较多”以上的学生约有400×30%=120人；
（3）选“A”的是一男一女，记作男1、女1，
根据题意可知：选择“D”的有4人且有2男2女，分别记作男2、男3、女2、女3，
列表如下：

	男2	男3	女2	女3
男1	（男1，男2）	（男1，男3）	（男1，女2）	（男1，女3）
女1	（女1，男2）	（女1，男3）	（女1，女2）	（女1，女3）

由上面可知共有4种可能，其中，1男1女的由4种，
则选择1名男生1名女生的概率为

4

8

=

1

2

．

点评：此题考查了条形统计图，扇形统计图，用样本估计总体，列表法与树状图法，弄清题意是解本题的关键．