题目内容
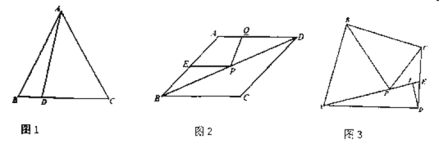
【题目】(1)如图1.等边的边长为2,点![]() 为
为![]() 边上一点,连接
边上一点,连接![]() ,则
,则![]() 长的最小值是________;
长的最小值是________;
(2)如图2,己知菱形![]() 的周长为16,面积为
的周长为16,面积为![]() ,
,![]() 为
为![]() 中点,若
中点,若![]() 为对角线
为对角线![]() 上一动点,
上一动点,![]() 为边
为边![]() 上一动点,计算
上一动点,计算![]() 的最小值;
的最小值;
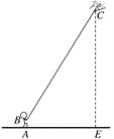
(3)如图3,己知在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 边上一个动点,连接
边上一个动点,连接![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,在
,在![]() 上截取
上截取![]() .试问在四边形
.试问在四边形![]() 内是否存在点
内是否存在点![]() ,使得
,使得![]() 的面积最小?若存在.请你在图中画出点
的面积最小?若存在.请你在图中画出点![]() 的位置,并求出
的位置,并求出![]() 的最小面积;若不存在,请说明理由.
的最小面积;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]() .
.
【解析】
(1)根据垂线段最短即可解决问题.
(2)如图2中,作AH⊥BC于H,在DC上截取DQ′=DQ,连接PQ′,AC,EC.首先证明△ABC是等边三角形,证明△PDQ≌△PDQ′(SAS),可得PQ=PQ′,推出PE+PQ=PE+PQ′,再根据垂线段最短即可解决问题.
(3)存在,如图3中,以AD为斜边在直线AD的下方作等腰直角△ADO,作OM⊥BC于M,AN⊥OM于N,连接AC,PD.证明点P的运动轨迹是![]() ,当点P在线段OM上时,PM的值最小,此时△PBC的面积最小.
,当点P在线段OM上时,PM的值最小,此时△PBC的面积最小.
解:(1)如图1中,根据垂线段最短可知,当AD⊥BC时,线段AD的值最小,
∵△ABC是等边三角形,
∴△ABC的高AD=![]() ,
,
∴AD的最小值为![]() .
.
故答案为:![]() .
.
(2)如图2中,作AH⊥BC于H,在DC上截取DQ′=DQ,连接PQ′,AC,EC.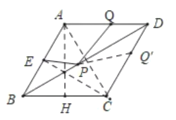
∵四边形ABCD是菱形,周长为16,
∴AB=BC=4,∠QDP=∠Q′DP,
∴S菱形ABCD=BCAH,
∴AH=![]() ,
,
∴sin∠ABH=![]() ,
,
∴∠ABH=60°,
∴△ABC是等边三角形,
∵AE=EB,
∴EC⊥AB,
∵DQ=DQ′,∠PDQ=∠PDQ′,DP=DP,
∴△PDQ≌△PDQ′(SAS),
∴PQ=PQ′,
∴PE+PQ=PE+PQ′,
根据垂线段最短可知,当E,P,Q′共线,且点Q′与C重合时,
PE+PQ′的值最小,最小值=EC=AH=![]() .
.
∴PE+PQ的值最小,最小值为:![]() .
.
(3)存在,理由如下:
如图3中,以AD为斜边在直线AD的下方作等腰直角△ADO,作OM⊥BC于M,AN⊥OM于N,连接AC,PD.
∵BA=BC=![]() ,∠ABC=90°,
,∠ABC=90°,
∴AC=![]() AB=8,∠BAC=45°,
AB=8,∠BAC=45°,
∵∠BAD=75°,
∴∠CAD=30°,
∴AD=ACcos30°=![]() ,
,
∵△ADO是等腰直角三角形,
∴OA=OD=![]() ,
,
∵∠ABM=∠NMB=∠ANM=90°,
∴四边形ABMN是矩形,
∴AB=MN=![]() ,∠BAN=90°,
,∠BAN=90°,
∴∠OAN=75°+45°90°=30°,
∴ON=![]() OA=
OA=![]() ,
,
∴OM=![]() ,
,
∵DF⊥AE,FP=FD,
∴∠FPD=45°,
∴∠APD=135°,
∴点P的运动轨迹是![]() ,
,
当点P在线段OM上时,PM的值最小,此时△PBC的面积最小,
此时PM=OMOP=![]() ,
,
∴△PBC的面积的最小值=![]() BCPM=
BCPM=![]()
![]()
![]() .
.