题目内容
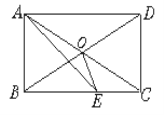
【题目】将两块大小一样含30°角的直角三角板，叠放在一起，使得它们的斜边AB重合，直角边不重合，已知AB=8，BC=AD=4，AC与BD相交于点E，连接CD．
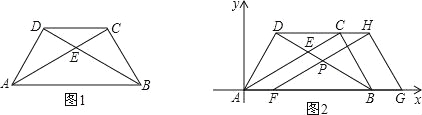
（1）填空：如图1，AC的长度= ，tan∠ABD= ；
（2）试判断△ADC与△AEB的关系，并说明理由；
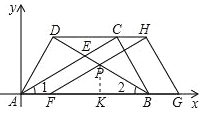
（3）如图2建立平面直角坐标系，保持△ABD不动，将△ABC向x轴的正方向平移到△FGH的位置，FH与BD相交于点P，设AF=t，△FBP面积为S，求S与t之间的函数关系式，并写出t的取值范围．
【答案】（1）4
，
；（2）△ADC∽△AEB，理由见解析；（3）S=
（8﹣t）2，t的取值范围为：0≤t＜8
【解析】
试题分析：（1）首先根据题意得：DC∥AB，∠ADB=∠ACB=90°，∠ABD=∠CAB=30°，然后由勾股定理，求得AC与BD的长，（2）根据两个含30°的直角三角板直接求出∠DAC=∠EAB=30°，∠AEB=∠ADC=120，即可得出△ADC∽△AEB．（3）过P作出△FBP的高．△FBP面积应等于FB×PK÷2，易得FB=AB﹣AF=8﹣t；则KB等于FB的一半，利用30°的正切值可求得FK的值．
试题解析：（1）根据题意得：DC∥AB，∠ADB=∠ACB=90°，∠ABD=∠CAB=30°，
∵AB=8，BC=AD=4，
∴AC=BD=4，∠ABD=30°，
∴tan∠ABD=tan30°=，
（2）△ADC∽△AEB，
理由：∵∠BAD=∠ABC=60°，∠BAC=∠ABD=30°，
∴∠DAC=∠CBD=∠BAC=30°，AE=BE，
∴∠AEB=180°﹣∠EAB﹣∠EBA=120°，
∵AC=BD，
∴ED=EC，
∴∠BDC=∠ACD=
（180°﹣∠DEC）=30°，
∵∠ADB=90°
∴∠ADC=∠ADB+∠BDC=120°=∠AEB，
∵∠DAC=∠BAC，
∴△ADC∽△AEB，
（3）（3）由题意知，FP∥AE，
∴∠1=∠PFB，
又∵∠1=∠2=30°，
∴∠PFB=∠2=30°，
∴FP=BP
过点P作PK⊥FB于点K，则FK=BK=FB．
∵AF=t，AB=8，
∴FB=8﹣t，BK=（8﹣t）．
在Rt△BPK中，PK=BKtan∠2=（8﹣t）tan30°=
（8﹣t）．
∴△FBP的面积S=FBPK=（8﹣t）（8﹣t），
∴S与t之间的函数关系式为：
S=（8﹣t）2，
t的取值范围为：0≤t＜8
