题目内容
【题目】如图，在矩形ABCD中，对角线AC，BD交于点E，DF⊥AC于F点，若∠ADF=3∠FDC，则∠DEC的度数是（ ）
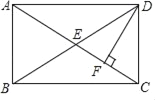
A. 30° B. 45° C. 50° D. 55°
【答案】B
【解析】
根据∠ADC=90°，求出∠CDF和∠ADF，根据矩形性质求出ED=EC，推出∠BDC=∠DCE，求出∠BDC，即可求出答案．
设∠FDC=x°，则∠ADF=3x°，
∵四边形ABCD是矩形，
∴∠ADC=90°，
∴x+3x=90，
x=22.5°，
即∠FDC=x°=22.5°，
∵DF⊥AC，
∴∠DFC=90°，
∴∠DCE=90°﹣22.5°=67.5°，
∵四边形ABCD是矩形，
∴AC=2EC，BD=2ED，AC=BD，
∴ED=EC，
∴∠BDC=∠DCE=67.5°，
∴∠BDF=∠BDC﹣∠CDF=67.5°﹣22.5°=45°，
∴∠DEC=90°﹣45°=45°
故选B．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
相关题目
