题目内容
(2004•南宁)期中考试后,学习小组长算出该组5位同学数学成绩的平均分为M,如果把M当成另一个同学的分数,与原来的5个分数一起,算出这6个分数的平均值为N,那么M:N为( )A.

B.1
C.

D.2
【答案】分析:根据5位同学数学成绩的平均分为M,求得5位同学的总分;再把M当成另一个同学的分数,与原来的5个分数一起,求得总分,再求这6个分数的平均值即为N;这样即可求得M与N的比值.
解答:解:∵5位同学数学成绩的平均分为M,
∴5位同学的总分为5M,
把M当成另一个同学的分数,与原来的5个分数一起,总分就为5M+M.
这6个分数的平均值= (5M+M)=M=N,
(5M+M)=M=N,
∴M:N=1.
故选B.
点评:本题考查了样本平均数的求法.所有数据的和除以这些数据的个数叫这些数据的平均数.
解答:解:∵5位同学数学成绩的平均分为M,
∴5位同学的总分为5M,
把M当成另一个同学的分数,与原来的5个分数一起,总分就为5M+M.
这6个分数的平均值=
 (5M+M)=M=N,
(5M+M)=M=N,∴M:N=1.
故选B.
点评:本题考查了样本平均数的求法.所有数据的和除以这些数据的个数叫这些数据的平均数.

练习册系列答案
相关题目
某校为了解八年级300名学生期中考的数学成绩,随机抽查了该年级50名学生的期中考数学成绩进行分析,绘制了不完整的频数分布表和频数分布直方图.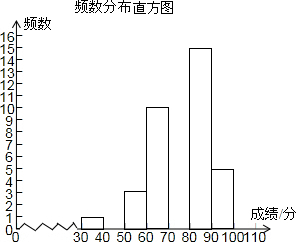
频数分布表
| 成绩分组 | 频 数 | 频 率 |
| 30≤x<40 | 1 | 0.02 |
| 40≤x<50 | 1 | 0.02 |
| 50≤x<60 | 3 | |
| 60≤x<70 | | 0.2 |
| 70≤x<80 | 15 | 0.3 |
| 80≤x<90 | 15 | 0.3 |
| 90≤x<100 | 5 | 0.1 |
| 合 计 | 50 | 1 |
(2)补全频数分布表和频数分布直方图;
(3)请你估计该校八年级期中考数学成绩优秀(不低于80分为优秀)的总人数.
某校为了解八年级300名学生期中考的数学成绩,随机抽查了该年级50名学生的期中考数学成绩进行分析,绘制了不完整的频数分布表和频数分布直方图.
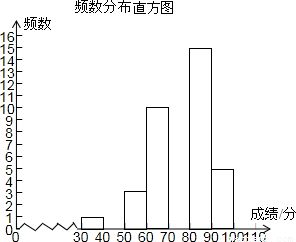
频数分布表
|
成绩分组 |
频 数 |
频 率 |
|
30≤x<40 |
1 |
0.02 |
|
40≤x<50 |
1 |
0.02 |
|
50≤x<60 |
3 |
|
|
60≤x<70 |
|
0.2 |
|
70≤x<80 |
15 |
0.3 |
|
80≤x<90 |
15 |
0.3 |
|
90≤x<100 |
5 |
0.1 |
|
合 计 |
50 |
1 |
(1)以上分组的组距= ;
(2)补全频数分布表和频数分布直方图;
(3)请你估计该校八年级期中考数学成绩优秀(不低于80分为优秀)的总人数.
(2004•南宁)某饮料厂为了开发新产品,用A、B两种果汁原料各19千克、17.2千克,试制甲、乙两种新型饮料共50千克,下表是试验的相关数据:
(1)假设甲种饮料需配制x千克,请你写出满足题意的不等式组,并求出其解集;
(2)设甲种饮料每千克成本为4元,乙种饮料每千克成本为3元,这两种饮料的成本总额为y元,请写出y与x的函数表达式,并根据(1)的运算结果,确定当甲种饮料配制多少千克时,甲、乙两种饮料的成本总额最少?
| 饮料 每千克含量 | 甲 | 乙 |
| A(单位:千克) | 0.5 | 0.2 |
| B(单位:千克) | 0.3 | 0.4 |
(2)设甲种饮料每千克成本为4元,乙种饮料每千克成本为3元,这两种饮料的成本总额为y元,请写出y与x的函数表达式,并根据(1)的运算结果,确定当甲种饮料配制多少千克时,甲、乙两种饮料的成本总额最少?