题目内容
如图,已知一次函数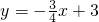 的图象与x轴,y轴分别相交于A,B两点,点C在AB上以
的图象与x轴,y轴分别相交于A,B两点,点C在AB上以 每秒1个单位的速度从点B向点A运动,同时点D在线段AO上以同样的速度从点A向点O运动,运动时间用t(单位:秒)表示.
每秒1个单位的速度从点B向点A运动,同时点D在线段AO上以同样的速度从点A向点O运动,运动时间用t(单位:秒)表示.
(1)求AB的长;
(2)当t为何值时,△ACD与△AOB相似并直接写出此时点C的坐标;
(3)△ACD的面积是否有最大值?若有,此时t为何值;若没有,请说明理由.
解:(1)当x=0时,y=3;当y=0时,x=4;
∴A(4,0),B(0,3),
∴OA=4,OB=3,
∴AB= =5;
=5;
(2)依题意BC=t,AC=5-t,AD=t,
若△ACD∽△ABO相似,
∴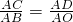 ,
,
代入得:
 =
= ,
,
解得:t= ,
,
若△ACD∽△AOB相似,
 ,
,
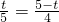 ,
,
解得t= ,
,
故C( ,
, )或(
)或( ,
, );
);
(3)∵AC=5-t,AD=t,而sin∠A= =
= ,
,
∴AD边上的高= (5-t),
(5-t),
∴S△ACD= ×AD×
×AD× (5-t)=
(5-t)= (5t-t2),
(5t-t2),
∴S△ACD有最大值,此时t=2.5,
∵S△ACD= (5t-t2)=-
(5t-t2)=- (t-2.5)2+
(t-2.5)2+ ,
,
∴当t=2.5时,S△ACD有最大值.
分析:(1)首先容易求出A,B两点的坐标,然后求出OA,OB的长度,再利用勾股定理求AB;
(2)先用t分别表示AC,AD的长度,再根据相似的性质可以列出关于t的方程,解方程就可以求出点C的坐标;
(3)用t表示△ACD的面积,然后利用二次函数求最大值.
点评:此题既考查了勾股定理的计算,也考查了相似三角形的性质,还有利用二次函数求最大值.
∴A(4,0),B(0,3),
∴OA=4,OB=3,
∴AB=
 =5;
=5;(2)依题意BC=t,AC=5-t,AD=t,
若△ACD∽△ABO相似,
∴
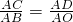 ,
,代入得:
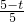 =
= ,
,解得:t=
 ,
,若△ACD∽△AOB相似,
 ,
,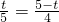 ,
,解得t=
 ,
,故C(
 ,
, )或(
)或( ,
, );
);(3)∵AC=5-t,AD=t,而sin∠A=
 =
= ,
,∴AD边上的高=
 (5-t),
(5-t),∴S△ACD=
 ×AD×
×AD× (5-t)=
(5-t)= (5t-t2),
(5t-t2),∴S△ACD有最大值,此时t=2.5,
∵S△ACD=
 (5t-t2)=-
(5t-t2)=- (t-2.5)2+
(t-2.5)2+ ,
,∴当t=2.5时,S△ACD有最大值.
分析:(1)首先容易求出A,B两点的坐标,然后求出OA,OB的长度,再利用勾股定理求AB;
(2)先用t分别表示AC,AD的长度,再根据相似的性质可以列出关于t的方程,解方程就可以求出点C的坐标;
(3)用t表示△ACD的面积,然后利用二次函数求最大值.
点评:此题既考查了勾股定理的计算,也考查了相似三角形的性质,还有利用二次函数求最大值.

练习册系列答案
相关题目
 如图,已知一次函数的图象经过A(-2,-1),B(1,3)两点.
如图,已知一次函数的图象经过A(-2,-1),B(1,3)两点. 如图,已知一次函数的图象经过点A(-1,0)、B(0,2).
如图,已知一次函数的图象经过点A(-1,0)、B(0,2). 在第一象限,CD⊥x轴于D,若OA=OB=OD=1.
在第一象限,CD⊥x轴于D,若OA=OB=OD=1. 的图象经过
的图象经过 ,
, 两点,并且交x轴于点C,交y轴于点D.
两点,并且交x轴于点C,交y轴于点D.
 的值;
的值; .
. 的图象与
的图象与 轴、
轴、 轴分别交于A、B两点且与反比例函数
轴分别交于A、B两点且与反比例函数 的图象在第一象限交于C点,CD⊥
的图象在第一象限交于C点,CD⊥ ,A B =
,A B =  ,C D =
,C D = 

