题目内容
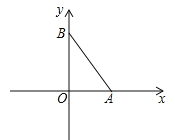
【题目】如图，在平面直角坐标系中，A、B两点分别在x轴、y轴上，OA=3，OB=4，连接AB．点P在平面内，若以点P、A、B为顶点的三角形与△AOB全等（点P与点O不重合），则点P的坐标为 ．
【答案】（3，4）或（
，
）或（
，
）．
【解析】
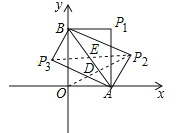
试题分析：如图所示：
①∵OA=3，OB=4，∴P1（3，4）；
②连结OP2，设AB的解析式为y=kx+b，则：
，解得：
．
故AB的解析式为
，则OP2的解析式为
，联立方程组得：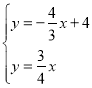
，解得
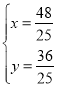，∴P2（，）；
③连结P2P3，∵（3+0）÷2=1.5，（0+4）÷2=2，∴E（1.5，2），∵1.5×2﹣=，2×2﹣=，∴P3（，）．
故点P的坐标为（3，4）或（，）或（，）．
故答案为：（3，4）或（，）或（，）．
练习册系列答案
相关题目
