题目内容
【题目】已知如图:抛物线y=x2﹣1与x轴交于A,B两点,与y轴交于点C.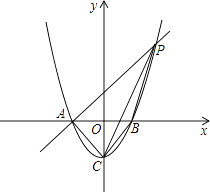
(1)求A,B,C三点的坐标.
(2)过点A作AP∥CB交抛物线于点P,求四边形ACBP的面积.
【答案】
(1)
解:∵令y=0,则x=±1,令x=0,则y=﹣1,
∴A(﹣1,0),B(1,0),C(0,﹣1)
(2)
解:设过B、C两点的直线解析式为y=kx+b(k≠0),
∵B(1,0),C(0,﹣1),
∴ ![]() ,解得
,解得 ![]() ,
,
∴直线BC的解析式为y=x﹣1,
∵AP∥CB,A(﹣1,0),
∴直线AP的解析式为:y=x+1,
∴ ![]() ,解得
,解得 ![]() 或
或 ![]() ,
,
∴P(2,3),
∴AP= ![]() =3
=3 ![]() ,
,
∵OB=OC=OA,∠BOC=90°,
∴△ABC是等腰直角三角形,即AC⊥BC,
∴四边形ACBP是直角梯形,
∵AC=BC= ![]() =
= ![]() ,
,
∴S四边形ACBP= ![]() (BC+AP)×AC=
(BC+AP)×AC= ![]() (
( ![]() +3
+3 ![]() )×
)× ![]() =4
=4
【解析】(1)先令y=0求出x的值即可得出AB两点的坐标;再令x=0,求出y的值即可得出C点坐标;(2)根据B、C两点的坐标用待定系数法求出直线BC的解析式,再根据AP∥CB,A(﹣1,0)可得出直线AP的解析式,故可得出点P的坐标,有两点间的距离公式可求出AP及BC的长,再根据OB=OC=OA,∠BOC=90°可知△ABC是等腰直角三角形,即AC⊥BC,再由梯形的面积公式即可得出结论.

练习册系列答案
相关题目